ные контактные напряжения определяются по формуле Прандтля (10)
при
k
=
k
1
. Случай
H/B
= 0
, т.е.
H
= 0
, отвечает решению Прандтля
с значениями
k
, выраженными в долях значения
k
1
поверхностного
упрочненного слоя. В этом можно убедить, обратившись к значениям
p
c
/
2
k
1
при
H/B
= 0
, приведенным в первом столбце табл. 1, которые
составляют соответствующие доли значений предельных контактных
напряжений, определяемых по формуле Прандтля (10) при
k
=
k
1
.
В работе [7] доказано, что при
H/B
>
1
,
579
, т.е. при достаточно
большой толщине поверхностного упрочненного слоя, деформируемая
полуплоскость ведет себя как однородная с
τ
max
=
k
1
. В этом случае на
предельные контактные напряжения
p
c
/
2
k
1
не влияет наличие более
мягкой, но достаточно глубоко расположенной от контакта, подложки.
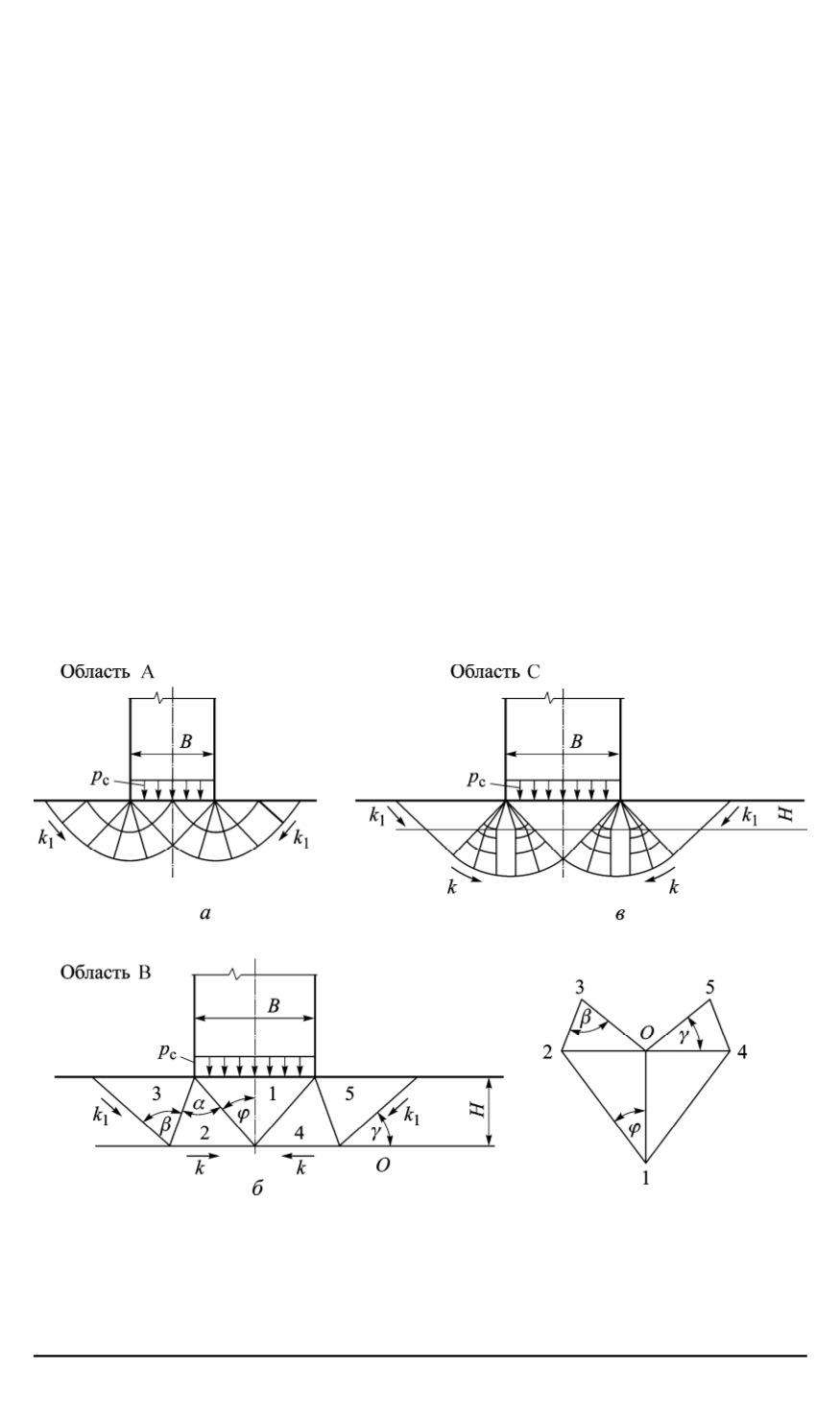
Поле линий скольжения в этом случае будет таким же, как и в класси-
ческом решении Прандтля для однородной полуплоскости (рис. 3,
а
).
При уменьшении отношения
H/B
наступает момент, когда пластиче-
ская область под пуансоном проникает через толщину поверхностного
слоя и выходит на границу раздела сред.
Наступление этого момента зависит не только от отношения
H/B
,
но и от значения отношения
k/k
1
[7]. В этом случае более мягкая под-
ложка играет роль своеобразной твердой смазки, по поверхности кото-
Рис. 3. Поля линий скольжения, используемые при решении задачи о вдавли-
вании плоского пуансона в пластически неоднородную полуплоскость:
а
— поля линий скольжения классического решения Прандтля;
б
— кинематическое
поле линий скольжения с годографом скоростей (для
H/B >
0
,
5
);
в
— поле линий
скольжения при
0
≤
H/B
≤
0
,
5
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2011. № 3 99


