слоем. Полное решение этой задачи для
H/B
≤
0
,
5
приведено в ра-
боте [9]. Поле линий скольжения этого решения показано на рис. 3,
а
,
а на рис. 3,
б
приведен годограф скоростей этой задачи. В работе [9]
доказано, что поле линий скольжений (см. рис. 3) определяет точные
значения предельных контактных нагрузок
p
c
, которые приведены в
табл. 2.
Описание примененной методики определения их численных зна-
чений содержится в работах [10, 11]. Отметим, что в случае
k/k
1
= 1
имеем однородную полуплоскость, отвечающую классическому реше-
нию Прандтля (1). Случай
H/B
= 0
также отвечает решению Пранд-
тля со значениями
k
, выраженными в долях от значения
k
1
поверх-
ностного упрочненного слоя (см. табл. 2).
В зависимости от значений указанных параметров
k/k
1
и
H/B
,
пластическая область может возникать либо в одном поверхностном
упрочненном слое, либо одновременно в поверхностном слое и в более
мягкой подложке [10–12], при этом на линии раздела указанных сред
имеют место разрывы нормальных напряжений
σ
x
[9].
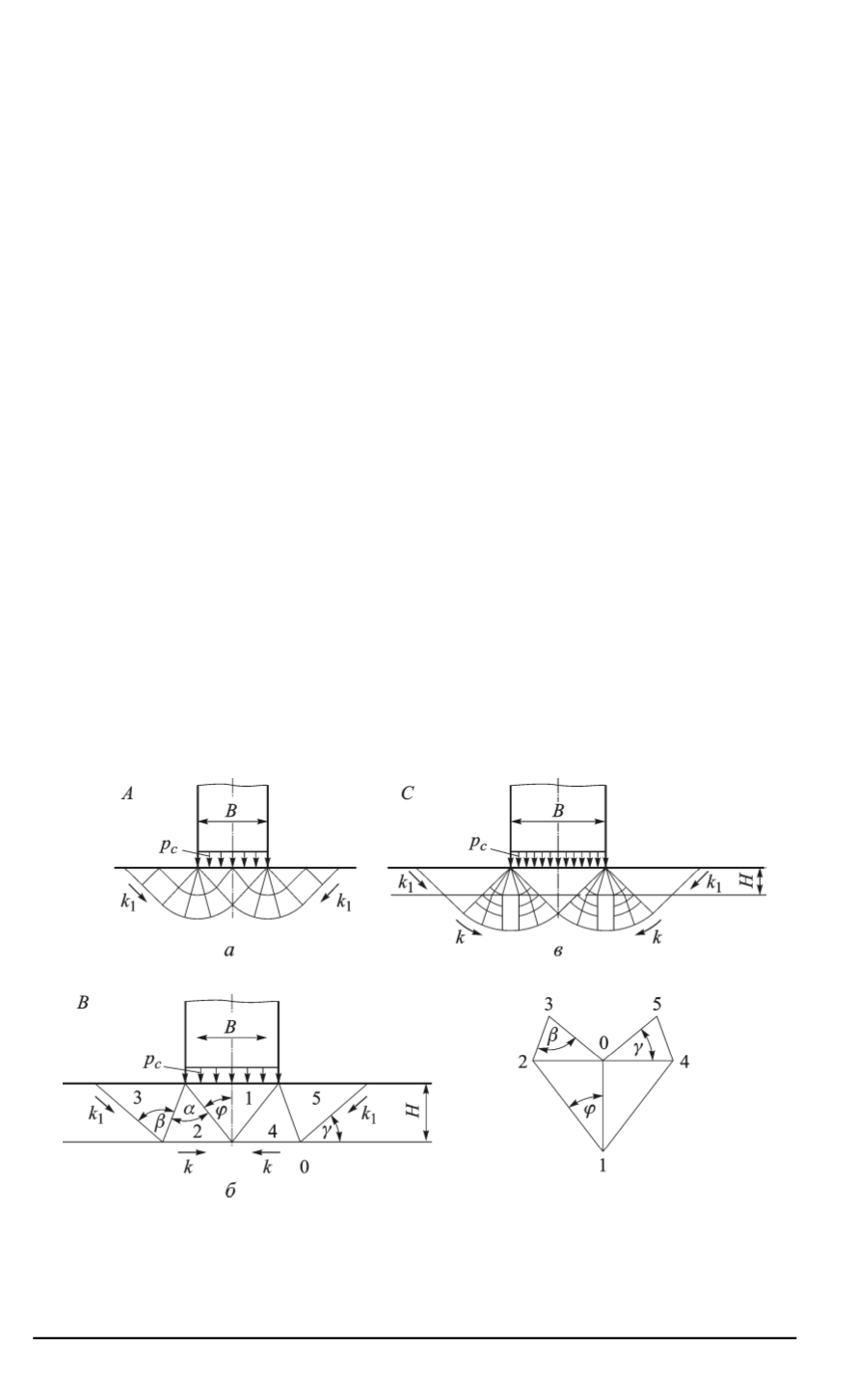
На рис. 4 области
A, B, C
отвечают трем возможным случаям рас-
положения пластической области при вдавливании жесткого плоско-
го пуансона в полуплоскость с поверхностным упрочненным слоем
[5, 12]. Области
A
и
A
1
относятся к случаю относительно большой
толщины
H/B
упрочненного слоя (рис. 5). Как следует из рисунка,
это будет всегда при
H/B
≥
1
,
579
. В этом случае вся пластическая
Рис. 4. Поля линий скольжений, используемые при решении задач о вдавлива-
нии плоских пуансонов в пластически неоднородную полуплоскость:
а
— поле линий скольжений классического решения Прандтля (область
А
);
б
—
кинематическое поле линий скольжений с годографом скоростей для
H/B >
0
,
5
(область
B
);
в
— поле линий скольжений при
0
≤
H/B
≤
0
,
5
(область
C
)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2012. № 4 113


