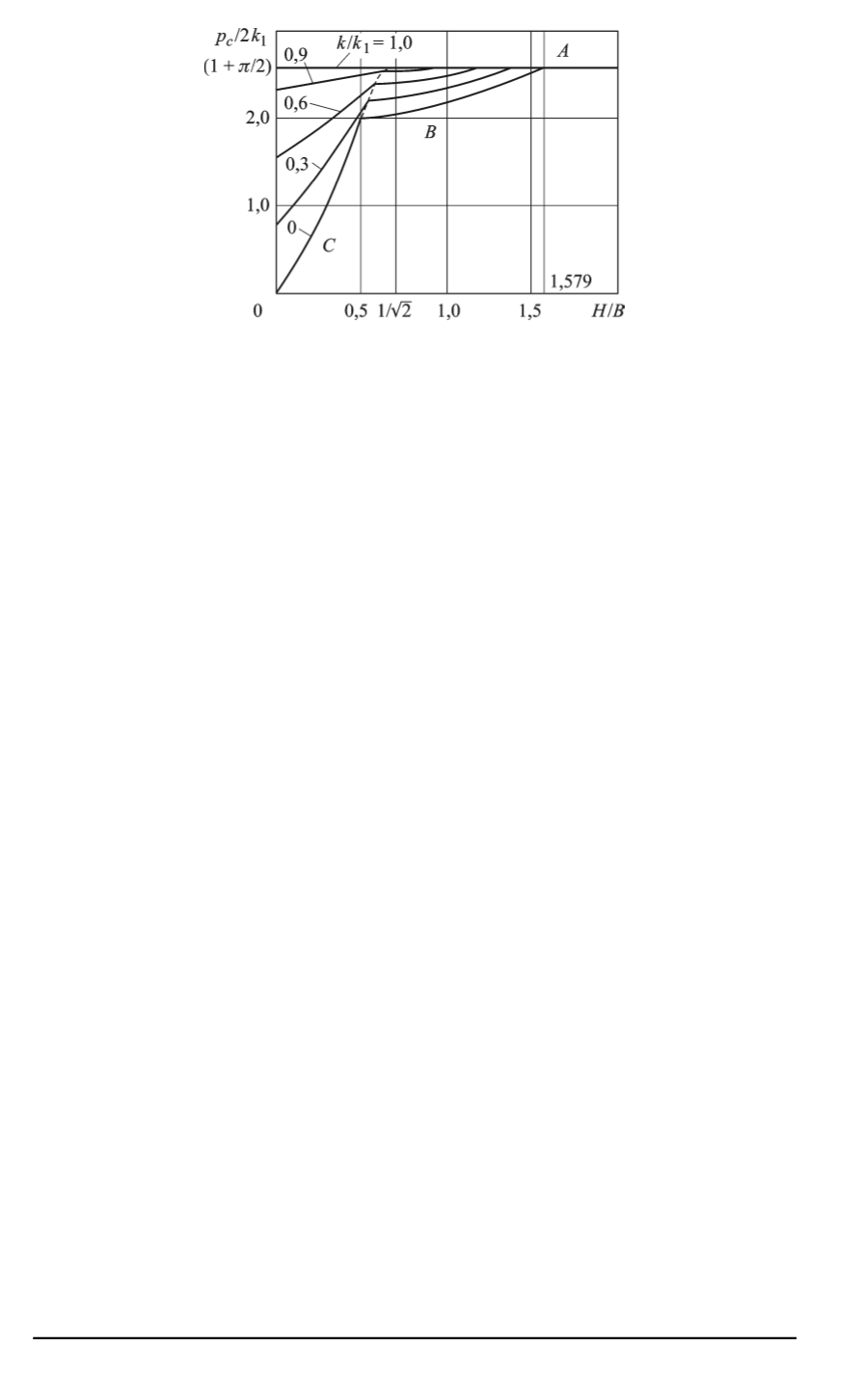
Рис. 5. Графики зависимостей предельных контактных давлений
p
c
/
2
k
1
от
отношения
H/B
для разных значений отношений пределов текучести на сдвиг
подложки
k
и поверхностного упрочненного слоя
k
1
область располагается в поверхностном упрочненном слое и реализу-
ется классическое решение Прандтля со значениями
p
c
/
2
k
1
, опреде-
ляемыми по формуле (1) при
k
=
k
1
.
Области
B
и
B
1
(рис. 4,
б
), относятся к меньшему значению отно-
шения
H/B
, когда пластическая область в поверхностном упрочнен-
ном слое выходит на линию раздела сред. Этот случай может возни-
кать только тогда, когда
H/B <
1
,
579
. Предельная нагрузка
p c/
2
k
1
в этом случае была определена с использованием численных мето-
дов решения оптимизационных задач, опирающихся на экстремальные
принципы теории пластичности [5]. Вычисленные значения
p
c
/
2
k
1
для
областей
B
и
B
1
приведены в табл. 3, а на рис. 5 показано изменение
предельных нагрузок
p
c
в рассматриваемом случае [5, 10, 12].
Дальнейшее уменьшение отношения
H/B
приводит к тому, что
пластическая область захватывает одновременно поверхностный упроч-
ненный слой и более мягкую подложку. В этом случае реализуется
точное решение, показанное на рис. 3, которому отвечают области
C
и
C
1
на рис. 6. Это решение справедливо для
0
≤
H/B
≤
0
,
5
, поэтому
для
H/B >
0
,
5
зависимости
p
c
/
2
k
1
от
H/B
(при
k/k
1
=
const) были
экстраполированы до области
B
. Вследствие практически линейного
характера зависимостей
p c/
2
k
1
= Φ(
H/B
)
для
H/B >
0
,
5
указанная
экстраполяция была выполнена линейным образом [5]. Вычисленные
предельные значения
p
c
/
2
k
1
, для последнего случая
C
приведены в
табл. 2.
В декартовой координатной системе
k/k
1
,
H/B
и
p
c
/
2
k
1
предель-
ные контактные напряжения
p
c
/
2
k
1
образуют поверхность предель-
ных напряжений, показанную на рис. 4,
а
в прямоугольной изометри-
ческой проекции [10–12]. В области
A
деформируемое тело ведет себя
как пластически однородная полуплоскость с
τ
max
=
k
1
. В области
B
при
H/B
≤
(
H/B
)
к1
пластическая область выходит на линию раздела
114 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2012. № 4


