При максимальных однонаправленных силах контактного трения
τ
к
=
k
,
m
= 1
и из формулы (6) получаем
p
τ
=
k
(1 +
π/
2) = (1
/
2)
p
c
,
т.е. предельные контактные давления в 2 раза меньше, чем в решении
Прандтля (1).
Из формул (1) и (6) определяем зависимость отношения
p
τ
/p
c
от
контактных сил трения, определяемых значениями параметра
m
:
p
c
/p
τ
= (1
/
2)[1 +
π/
2 + arccos
m
+ sin(arccos
m
)](1 +
π/
2)
−
1
.
(7)
На рис. 1,
в
показан график зависимости отношений
p
τ
/p
c
от пара-
метра
m
, отвечающий формуле (7), численные значения которого при-
ведены в табл. 1. Для пластически однородных твердых тел диапазон
изменения отношения
p
τ
/p
c
в формуле (7) составляет
1
≥
p
τ
/p
c
≥
0
,
5
при
0
≤
τ
к
≤
k
соответственно.
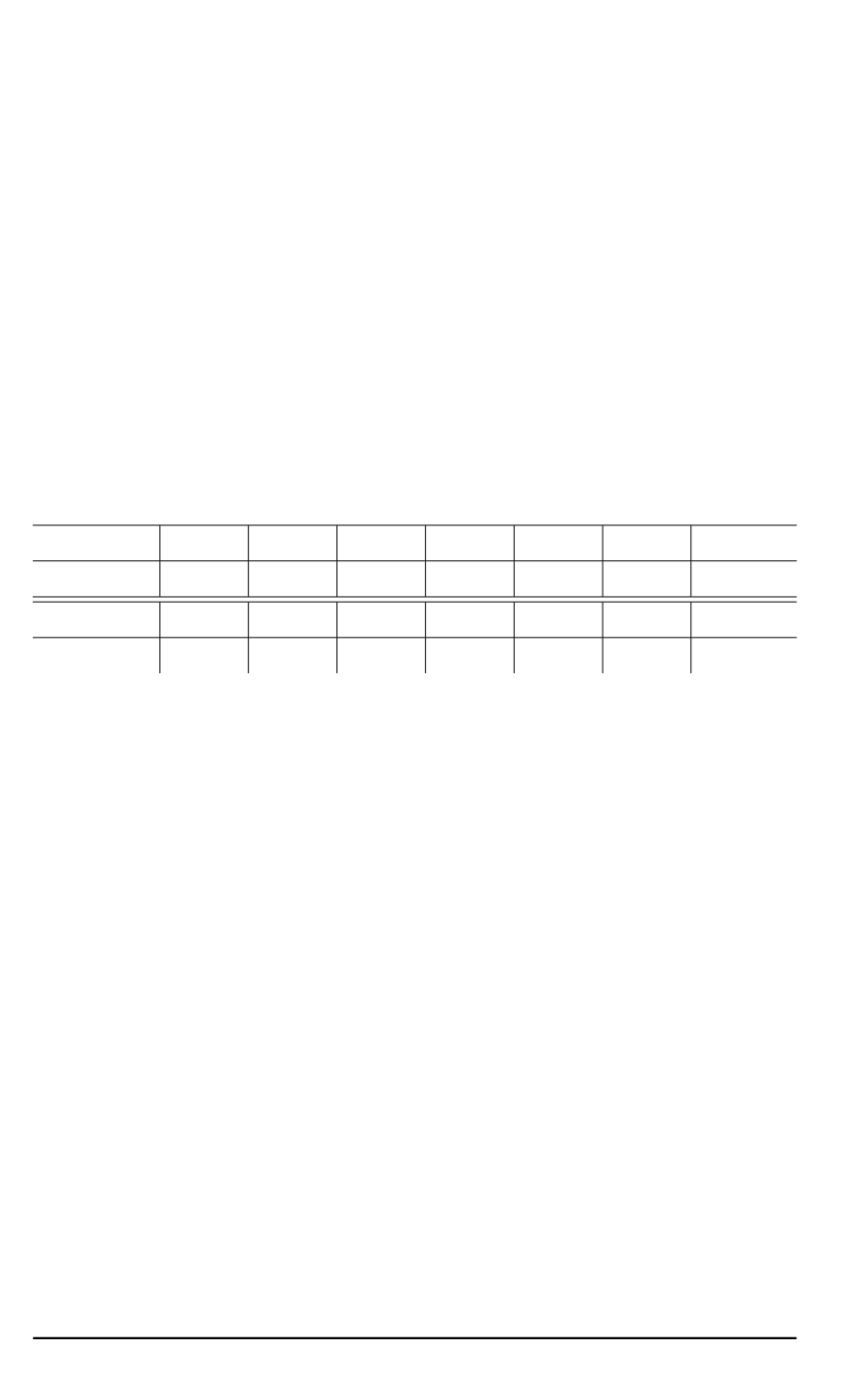
Таблица 1
Влияние однонаправленных контактных касательных сил трения
τ
к
на
нормальные предельные напряжения
p
τ
m
=
τ
к
/k
0
0,1
0,2
0,3
0,4
0,5
0,6
p
τ
/p
c
1,0 0,980 0,957 0,932 0,904 0,872 0,836
m
=
τ
к
/k
0,7
0,8
0,85 0,90 0,95 0,975 1,0
p
τ
/p
c
0,794 0,742 0,710 0,672 0,622 0,587 0,5
Основной результат проведенных исследований состоит в том, что
для пластически однородных твердых тел различной начальной глад-
кой формы базовые значения предельных контактных давлений лежат
внутри узкого диапазона, определяемого неравенствами (2), (3). Вли-
яние кривизны свободной поверхности, примыкающей к контактной
области, учитывается изменением границ интервалов (2), (3) [4, 5].
Сравнение предельных значений
p
c
, определяемых по второму
стандартному методу упругого расчета и по методу предельных
контактных напряжений
p
c
.
Обратимся к рассмотрению принципи-
ально важного вопроса о количественном соотношении значений пре-
дельных контактных напряжений
p
c
, определяемых во втором методе
расчета контактной прочности, т.е. на основе чисто упругих реше-
ний, и в третьем, новом предлагаемом методе расчета по предельным
контактным нагрузкам
p
c
.
При контакте двух упругих тел задача, аналогичная плоскому ре-
шению Прандтля, получается при вдавливании длинного кругового
цилиндра в упругое полупространство (см. рис. 2,
а
). Рассмотрим си-
ловой контакт указанных упругих тел. Первое тело — круговой ци-
линдр радиусом
R
и длиной
L
(
L
≥
R
), второе тело — упругое полу-
пространство. При равенстве модулей упругости
E
1
=
E
2
=
E
у обоих
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2012. № 4 105


