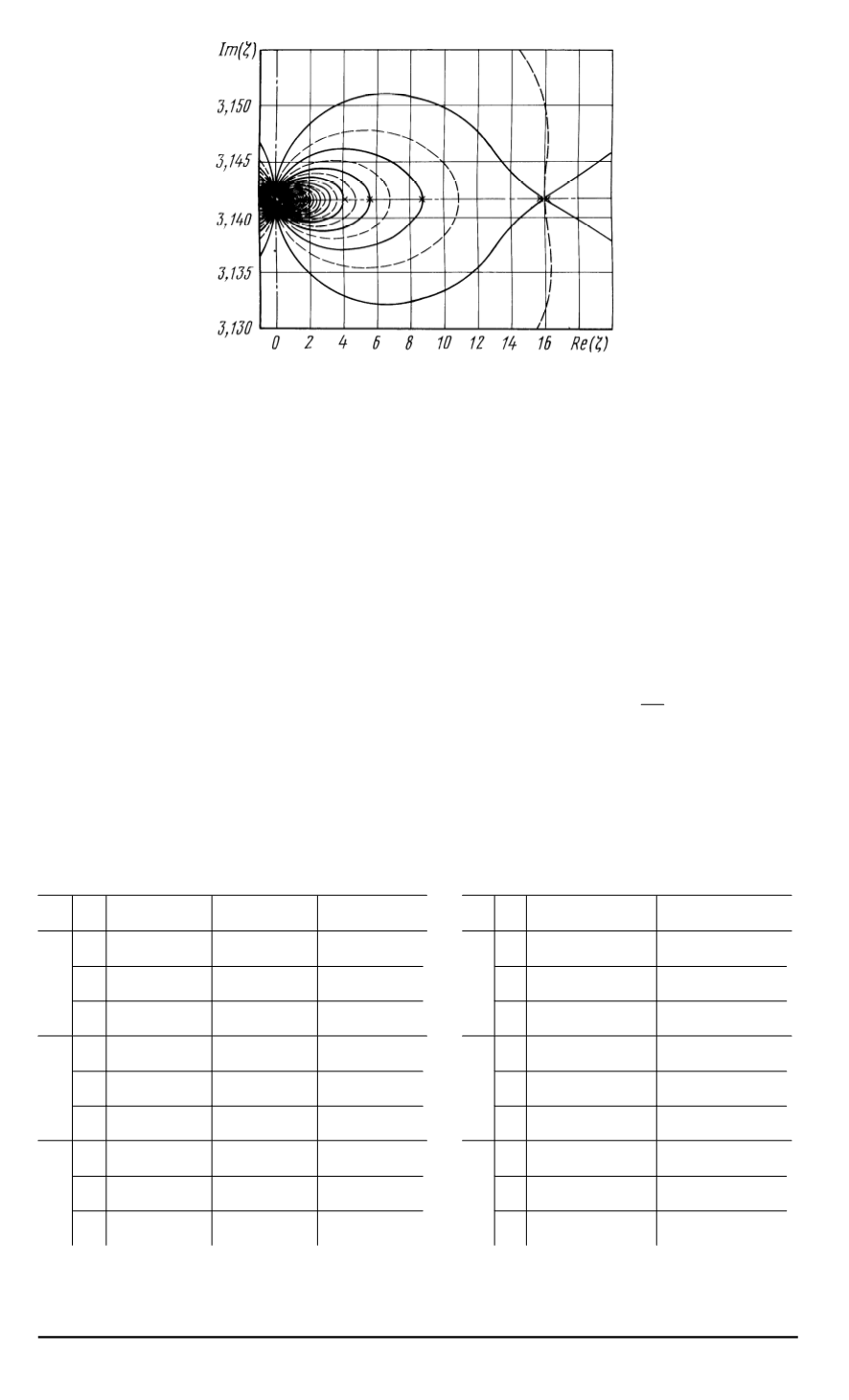
Рис
. 3.
Графическое решение уравнений
(33)
и
(34)
для внутренних волн и волн
на свободной поверхности
:
m
= 0
,
¯
H
= 2
, r
0
= 0
,
1
,
β
= 0
,
1
отметить
,
что качественно это решение сходно с решением для коакси
-
ального цилиндра
,
за исключением дополнительной группы корней
,
от
-
вечающей поверхностным волнам
.
При данном соотношении исходных
параметров существуют две группы действительных решений
—
стре
-
мящихся к бесконечности и к
0 (
точки
1
и
2
,
см
.
рис
. 2).
Внутренние и
поверхностные волны характеризуются комплексными числами
,
груп
-
пирующимися вдоль мнимой оси
ζ
(
области
3
и
4
,
см
.
рис
. 2,
и корни
,
отмеченные знаком
“*”,
на рис
. 3),
с точкой накопления
i
lπ
H
.
Численные
значения решений приведены в табл
. 1–4 (
при
m
= 0
;
¯
H
= 2
;
β
= 0
,
1
).
Таблица
1
Волны слива
(
Re
(
ζ
)
→ ∞
).
Результаты вычисления
ζ
,
ξ
и
λ
n R
0
= 0
,
1
R
0
= 0
,
3
R
0
= 0
,
5
ζ
1,09723 1,74562 2,71861
1
ξ
1,10201 1,74849 2,72044
λ
10,7032 17,4238 27,1850
ζ
4,97777 6,56750 9,29099
2
ξ
4,97877 6,56827 9,29153
λ
49,7777 65,6750 92,9099
ζ
8,55366 11,1199 15,6278
3
ξ
8,55424 11,1204 15,6282
λ
85,5366 111,199 156,278
Таблица
2
Волны слива
(
Re
(
ζ
)
→
0
).
Результаты вычисления
ζ
,
ξ
и
λ
n
R
0
= 0
,
1
R
0
= 0
,
3
ζ
0,0487210 0,0329412
1
ξ
1,03065
1,520410
λ
0,0473251 0,0216711
ζ
0,0103548 0,00834263
2
ξ
4,82940
5,99388
λ
0,00214412 0,00139186
ζ
0,00600572 0,00487969
3
ξ
8,32581
10,24691
λ
0,000721338 0,000476212
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2004.
№
1 13


