Для изучения поверхностных волн и получения приближенных
асимптотических решений
,
удобнее воспользоваться предыдущей си
-
стемой несколько другого вида
.
Перейдем от функций Бесселя
J
и
Y
к
модифицированным функциям Бесселя
I
и
K
.
Пусть
α
=
iξ
.
Окончательно система примет вид для случая
m
= 0
F
0
(
α
) +
4
α
2
r
0
(
µ
2
l
−
α
2
)
G
0
(
α
) = 0
,
(32)
где
F
0
(
α
) =
α
[
K
1
(
α
)
I
1
(
r
0
α
)
−
K
1
(
r
0
α
)
I
1
(
α
)];
G
0
(
α
) =
K
0
(
r
0
α
)
I
1
(
α
) +
K
1
(
α
)
I
0
(
r
0
α
)
.
Случай стоячих волн
,
m
= 0
.
Исключая
λ
из уравнений
(29)–(31),
получим систему трансцендентных уравнений относительно неизвест
-
ных
ξ
и
ζ
:
ξ
[
J
1
(
ξ
)
Y
1
(
ξr
0
)
−
Y
1
(
ξ
)
J
1
(
ξr
0
)]
−
−
4
ξ
2
r
0
(
ξ
2
−
ζ
2
)
[
Y
1
(
ξ
)
J
0
(
ξr
0
)
−
J
1
(
ξ
)
Y
0
(
ξr
0
)] = 0;
(33)
tanh(
ζ
¯
H
) =
β
p
ξ
2
−
ζ
2
,
β
=
1
¯
γ
.
(34)
Эту систему можно представить в виде одного комплексного уравнения
относительно комплексной переменной
ζ
,
выразив
ξ
через
ζ
из второго
уравнения
µ
ξ
=
s
ζ
2
+
β
2
tanh
2
ζ
¯
H
¶
.
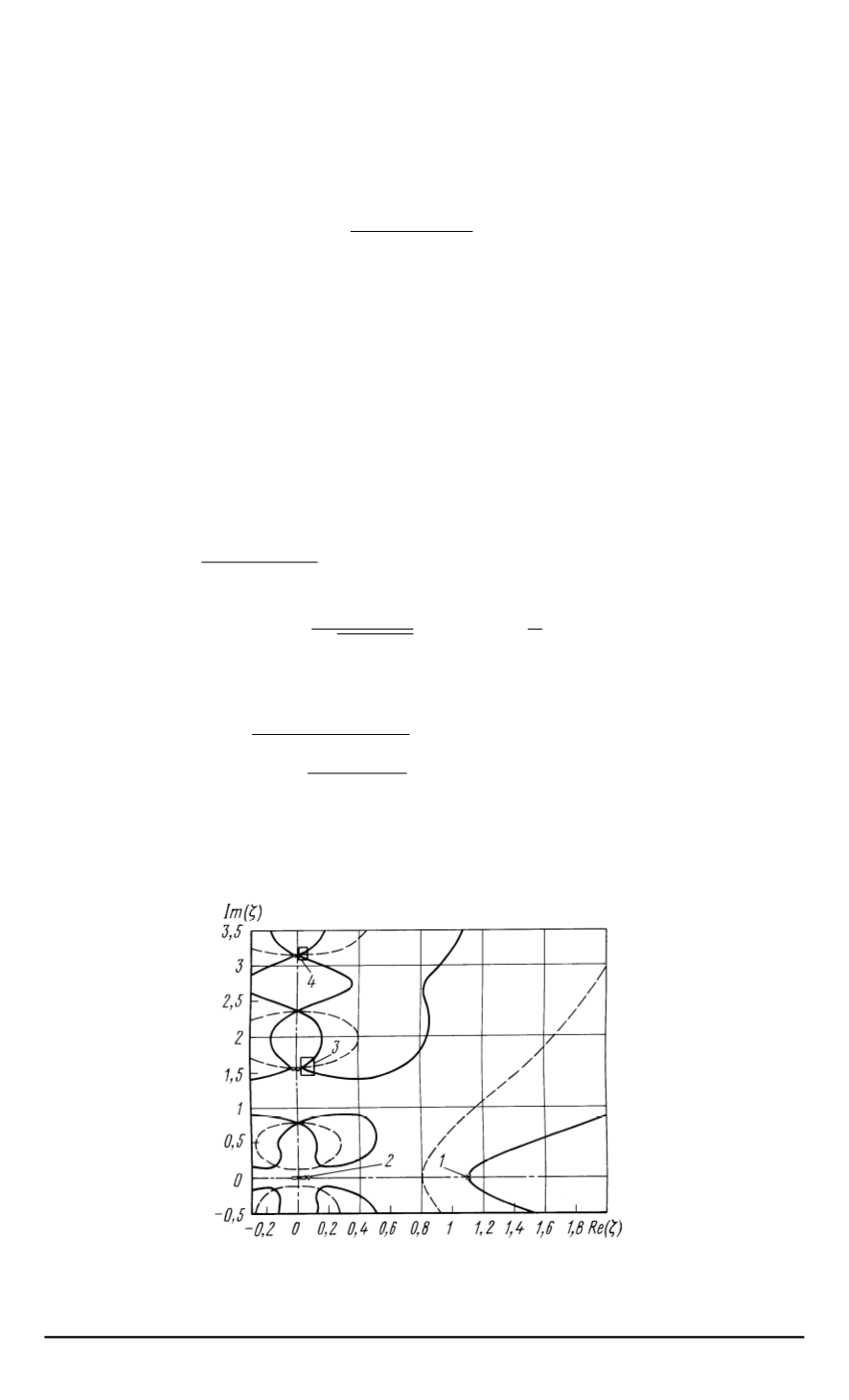
Графическое решение этой систе
-
мы уравнений позволяет выделить несколько групп корней в зависи
-
мости от их расположения на комплексной плоскости
(
рис
. 2).
Можно
Рис
. 2.
Графическое решение уравнений
(33)
и
(34)
в плоскости комплексного
переменного
ζ
:
m
= 0
,
¯
H
= 2
, r
0
= 0
,
1;
β
= 0
,
1
12 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2004.
№
1


