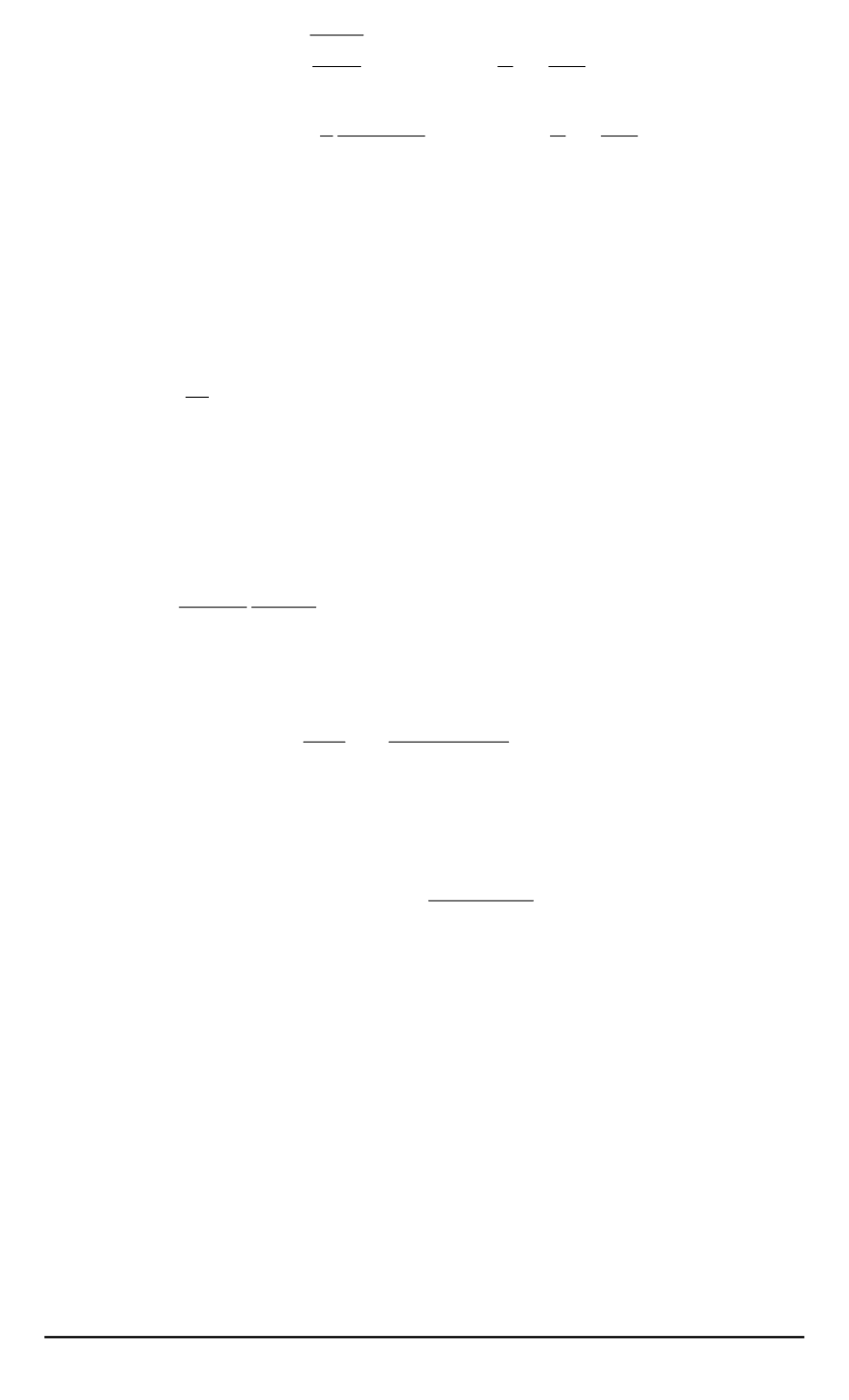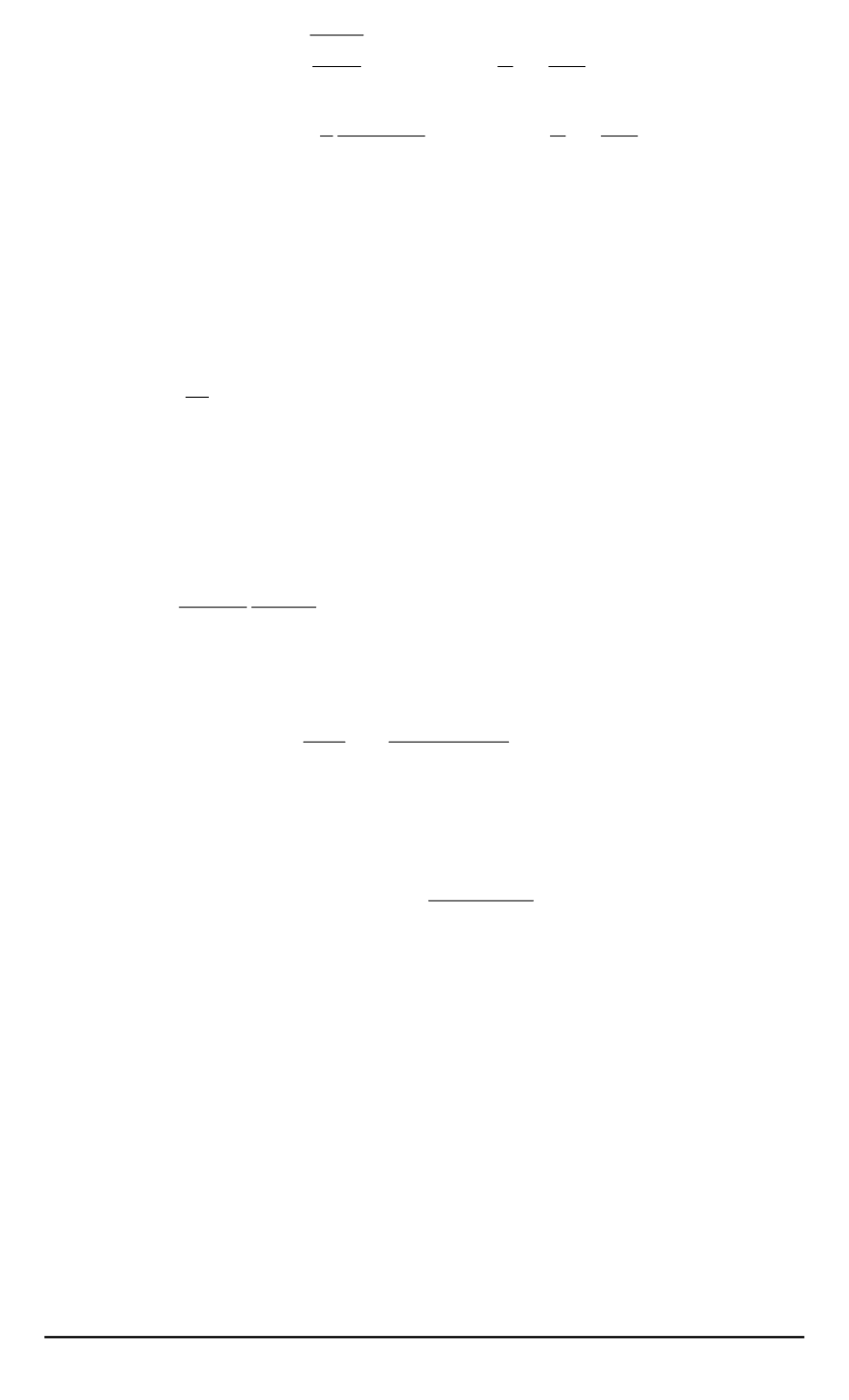
Y
m
(
ξr
0
)
³
r
2
πr
0
ξ
µ
sin
³
ξr
0
−
π
4
−
mπ
2
´
+
+
1
8
4
m
2
−
1
ξr
0
cos
³
ξr
0
−
π
4
−
mπ
2
´ ¶
.
Подставляя эти разложения в уравнение
(29),
получим следующее
асимптотическое уравнение для чисел
ξ
и
ζ
:
tan(
ξ
(
r
0
−
1)) = Φ(
ξ, ζ, m,
¯
γ, r
0
) +
i
¯
γ
−
1
Ψ(
ξ, ζ , m,
¯
γ, r
0
)
,
(39)
где
Φ
и
Ψ
—
дробно
-
рациональные функции волновых чисел
ξ, ζ, m
.
В случае отсутствия слива
(
¯
γ
→ ∞
),
волновые числа
ζ
оказываются
равны
ζ
=
i
πl
¯
H
, l
= 1
,
2
, . . .
,
а тран
c
цендентное уравнение
(39)
име
-
ет только действительные решения
,
определяющие волновые числа
ξ
внутренних волн
.
Решение уравнения
(39)
в комплексной плоскости
ξ
представим в
виде
ξ
=
ξ
0
+
ε,
(40)
где
ξ
0
=
2
q
−
1
2
π
1
−
r
0
,
q
=
q
0
, q
0
+ 1
, . . .
—
корни уравнения
cot(
ξ
0
(1
−
r
0
)) = 0
.
Подставив выражение
(40)
в уравнение
(39),
опре
-
делим поправку
ε
и окончат
e
льное асимптотическое выражение для
ξ
:
ξ
=
ξ
q
µ
1 +
A
ξ
2
q
C
+
i
m
ξ
3
q
¯
γ
(
r
0
−
1)
¶
,
q
→ ∞
,
где
A
= 4
m
2
¯
γ
2
(
r
0
−
1) + ¯
γ
2
+ 2
r
2
0
+ 3
r
0
¯
γ
2
,
C
= 8
r
0
¯
γ
2
(
r
0
−
1)
.
Для случая
m
= 0
имеем приближенное решение
ξ
q
=
ξ
(0)
q
−
r
0
(1
−
r
0
)
4¯
γ
2
ξ
(0)
q
.
Обсуждение результатов решения
.
При анализе полученных ре
-
зультатов следует отметить появление решений
,
не встречающихся в
задачах без слива
,
а также изменение традиционных решений под влия
-
нием наличия слива
.
Прежде всего
,
наличие поверхности слива опреде
-
ляет возможность появления на ней волновых движений
—
волн слива
.
Причины их появления впервые рассматривались в работе
[9].
Волны
слива характеризуются волновыми и собственными числами
—
реше
-
ниями соответствующих систем уравнений
.
В общем случае
,
это апе
-
риодические затухающие волновые движения
.
Появление в системе по
-
верхности слива также отражается и на существующих в ней колеба
-
тельных движениях
.
Внутренние волны и волны на свободной поверх
-
ности превращаются в затухающие волновые движения
.
18 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2004.
№
1