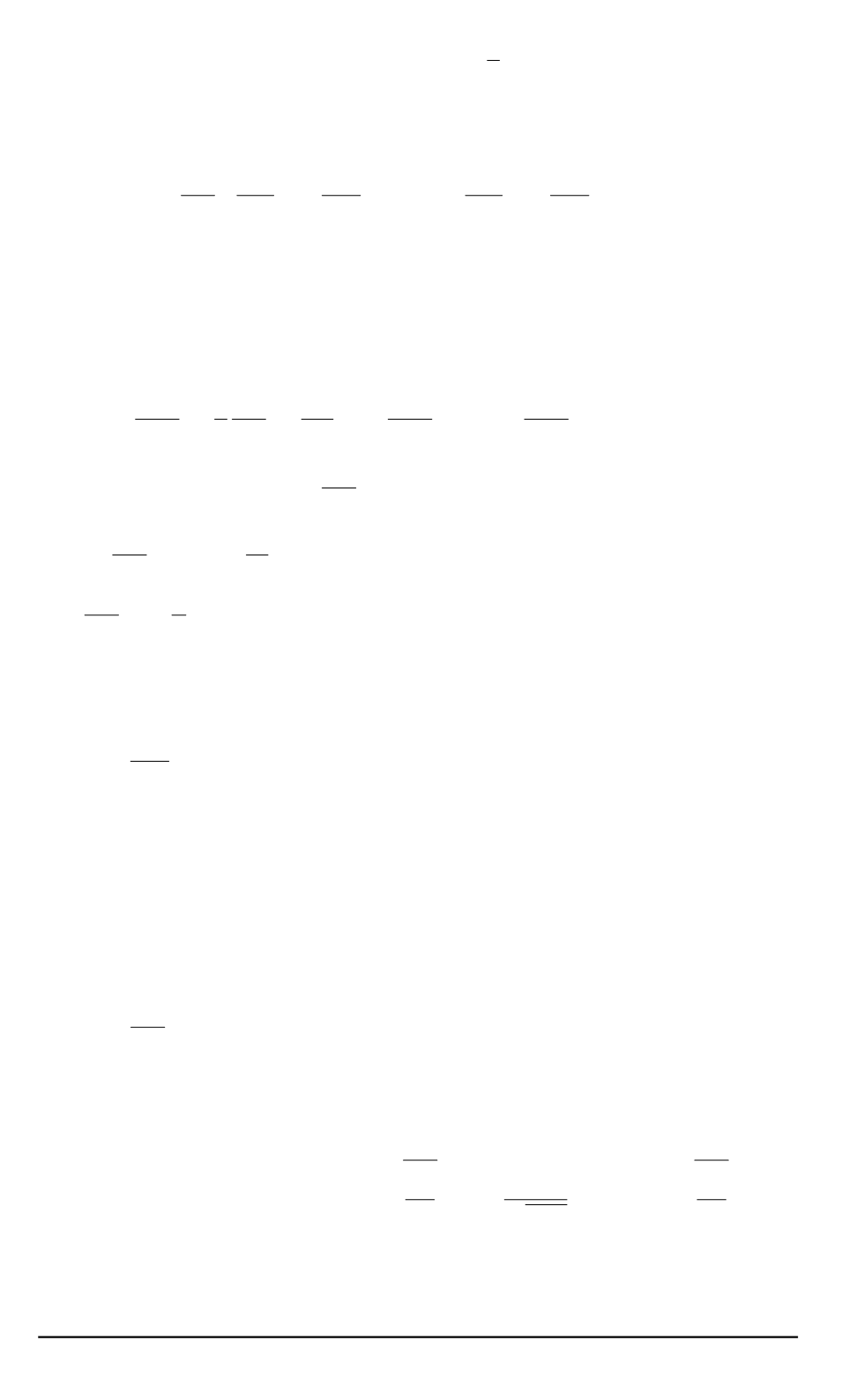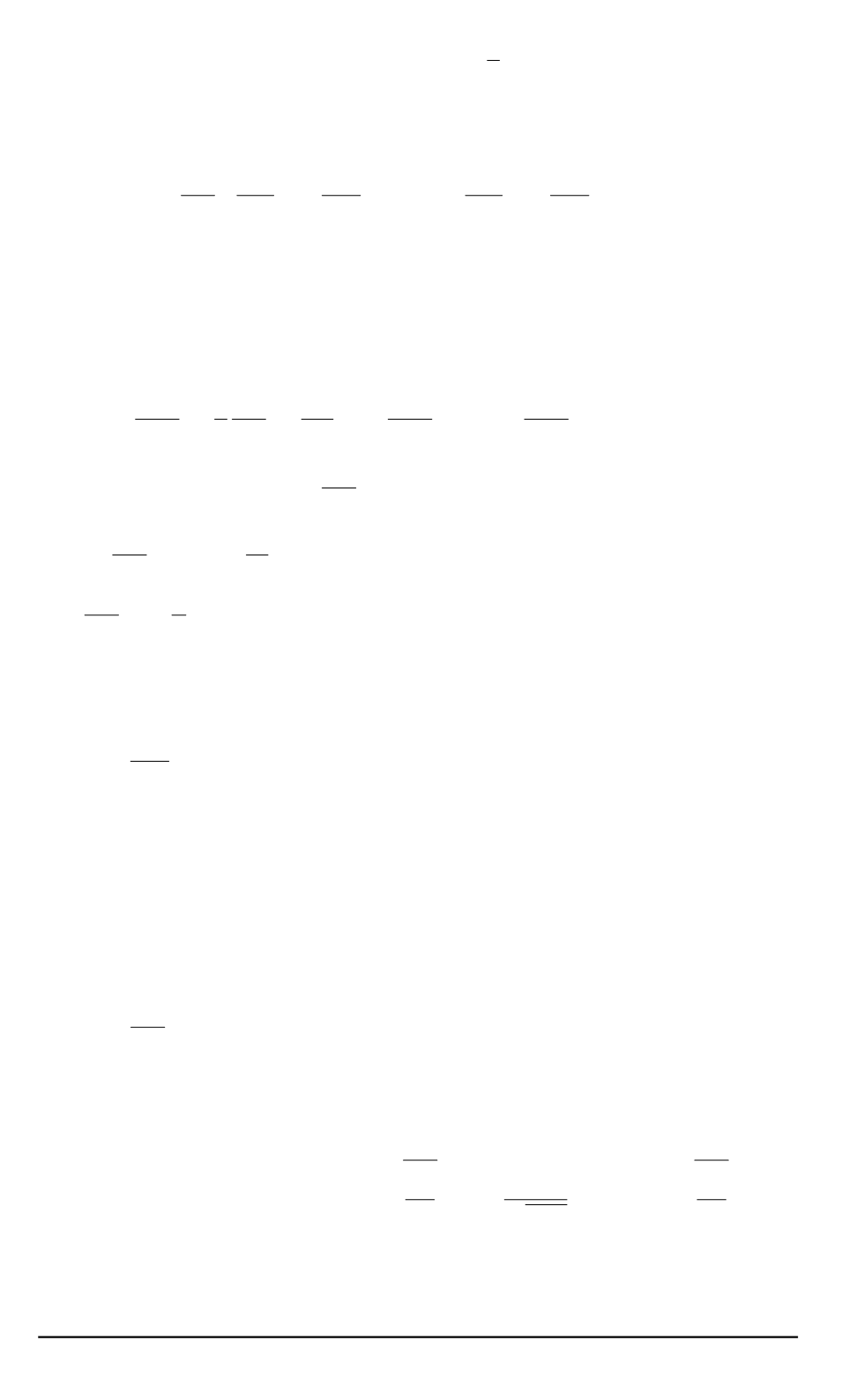
возмущенного давления
,
p
0
вместо
p
0
=
1
2
ω
2
0
r
2
−
gx
3
+
C
,
можно ис
-
пользовать
p
0
=
−
gx
3
+
C
и соответственно
|∇
p
0
|
=
g
.
Учитывая это
допущение
,
соотношение
(8)
можно представить в виде
∂
2
∂t
2
·
∂
2
p
∂t
2
+
g
∂p
∂x
3
¸
+ 4
ω
2
0
·
∂
2
p
∂t
2
+
g
∂p
∂x
3
¸
= 0
.
Рассмотрим задачу о собственных движениях жидкости
.
Будем
искать решение в виде бегущих волн
p
(
r, η, x, t
) =
P
(
r, x
)
e
(
imη
−
Ω
t
)
,
m
= 0
,
±
1
,
±
2
, . . .
.
Тогда
,
вместо системы
(7)–(11),
для каждого задан
-
ного числа
m
получим спектральную задачу
:
Ω
2
µ
∂
2
P
∂r
2
+
1
r
∂P
∂r
−
m
2
r
2
P
+
∂
2
P
∂x
2
¶
+ 4
ω
2
0
∂
2
P
∂x
2
= 0
в
Q,
(12)
¡
Ω
2
+ 4
ω
2
0
¢ µ
Ω
2
P
+
g
∂P
∂x
¶
= 0
на
Γ
0
,
(13)
Ω
2
∂P
∂r
−
2
ω
0
Ω
i
m
r
P
= 0
на
S,
(14)
∂P
∂x
+ Ω
1
γ
P
= 0
на
Σ
,
(15)
m
= 0
,
±
1
,
±
2
, . . .
При отсутствии свободной поверхности
(
условие
(8)
заменяется на
условие
∂p
∂x
3
= 0
на
Γ
0
)
получаем задачу
,
приведенную в работах
[9, 10].
Здесь
Ω
—
комплексный коэффициент затухания волновых движений
жидкости
.
Если положить
Im
Ω
>
0
,
то число
m <
0
будет соответ
-
ствовать прямым волнам
,
бегущим в сторону вращения жидкости
,
чи
-
сло
m >
0
—
обратным волнам
,
а число
m
= 0
—
случаю стоячих
волн
.
В дальнейшем нас не будут интересовать решения
,
при которых
Ω = 2
ω
0
i
.
Поэтому граничное условие
(13)
можно переписать в виде
Ω
2
P
+
g
∂P
∂x
= 0
.
Вывод характеристических уравнений задачи
.
Пусть
R
0
—
харак
-
терный размер
.
Введем безразмерные параметры
ζ, ξ, λ,
¯
γ, ε
при помо
-
щи соотношений
ζ
=
µR
0
;
ξ
=
kR
0
;
λ
= Ω
s
R
0
g
; ¯
γ
=
γ
√
gR
0
;
ε
= 2
ω
0
s
R
0
g
,
где безразмерные параметры
ζ
и
ξ
характеризуют движения жидкости
соответственно в осевом и радиальном направлениях и связаны с соб
-
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2004.
№
1 5