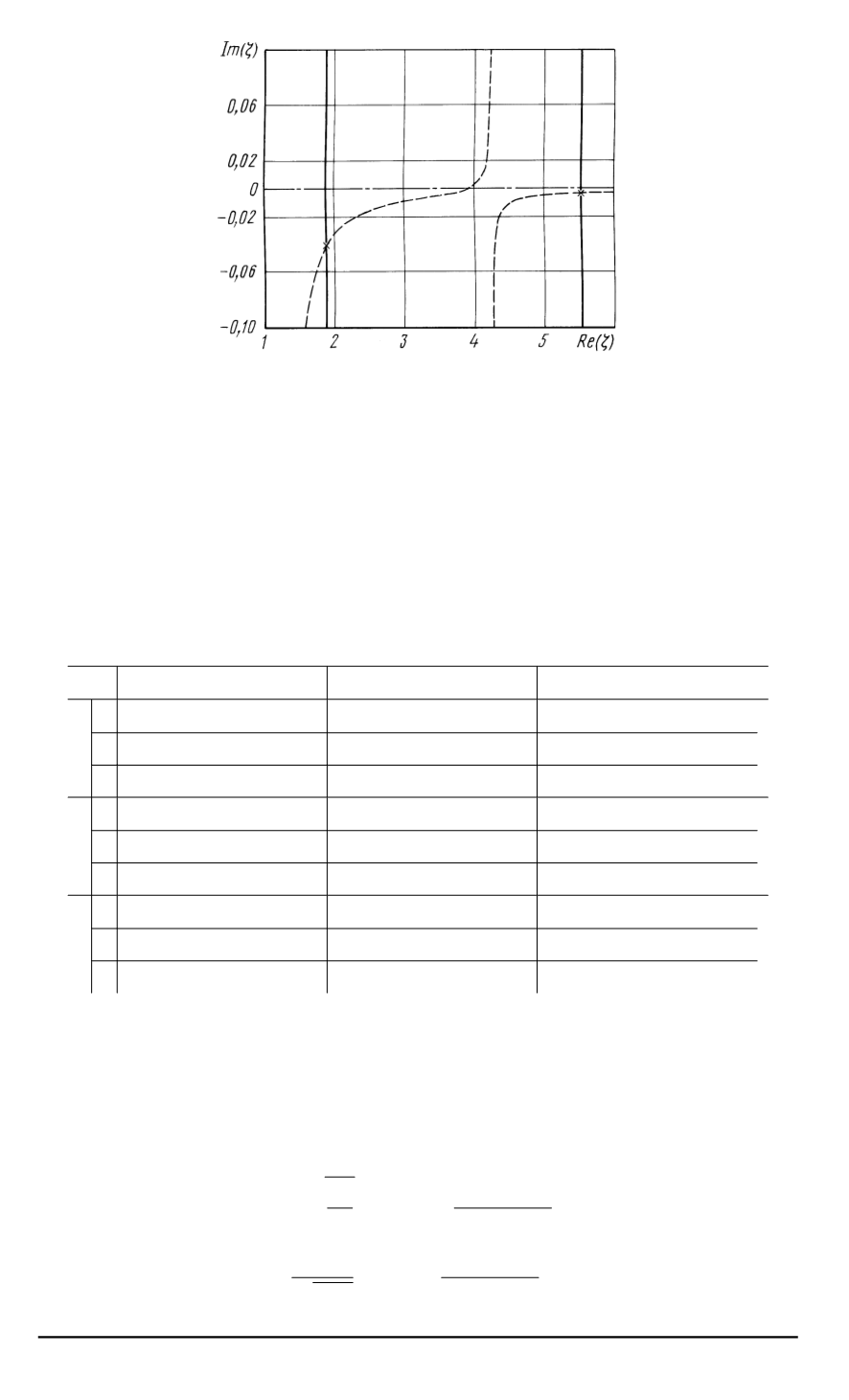
Рис
. 4.
Графическое решение уравнения
(57)
для волн слива
:
m
= 1
,
¯
H
= 2
,
β
= 0
,
1
обратных волн
.
В случае бегущих волн действительные решения
,
отве
-
чающие волнам на поверхности слива
,
становятся комплексными
.
Это
хорошо видно на рис
. 4
и из табл
. 5–7 (
при
m
= 1
;
¯
H
= 2
;
β
= 0
,
1
).
Таблица
5
Волны слива
(
Re
(
ζ
)
→ ∞
).
Результаты вычисления
ζ
,
ξ
и
λ
n
R
0
= 0
,
1
R
0
= 0
,
3
R
0
= 0
,
5
ζ
1,87826 – 0,0411437
i
2,19093 – 0,0352369
i
2,97048 – 0,0252734
i
1
ξ
1,88093 – 0,0410845
i
2,19321 – 0,0352000
i
2,97216 – 0,0252591
i
λ
18,7624 – 0,414350
i
21,9025 – 0,353222
i
29,7043 – 0,252772
i
ζ
5,53129 – 0,00360453
i
6,78825 – 0,00309701
i
9,393623 – 0,00227862
i
2
ξ
5,53219 – 0,00360394
i
6,78899 – 0,00309667
i
9,39416 – 0,00227849
i
λ
55,3129 – 0,0360453
i
67,8825 – 0,0309701
i
93,9362 – 0,0227862
i
ζ
8,97410 – 0,00136230
i
11,2614 – 0,00112431
i
15,6907 – 0,000813715
i
3
ξ
8,97465 – 0,00136222
i
11,2619 – 0,00112427
i
15,6910 – 0,000813699
i
λ
89,7410 – 0,0136230
i
112,614 – 0,0112431
i
156,907 – 0,00813715
i
Асимптотика больших индексов
.
Поверхностные волны
.
Получим
здесь асимптотические формулы для определения волновых чисел и
частот поверхностных волн и волн слива соответственно при
l
→ ∞
и
n
→ ∞
.
Используя асимптотические разложения
[11]
для
I
m
(
z
)
и
K
m
(
z
)
,
имеем
K
m
(
z
) =
r
π
2
z
e
−
z
½
1 +
4
m
2
−
1
2
1! 8
z
+
. . .
¾
;
(36)
I
m
(
z
) =
1
√
2
πz
e
z
½
1
−
4
m
2
−
1
2
1! 8
z
+
. . .
¾
.
(37)
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2004.
№
1 15


