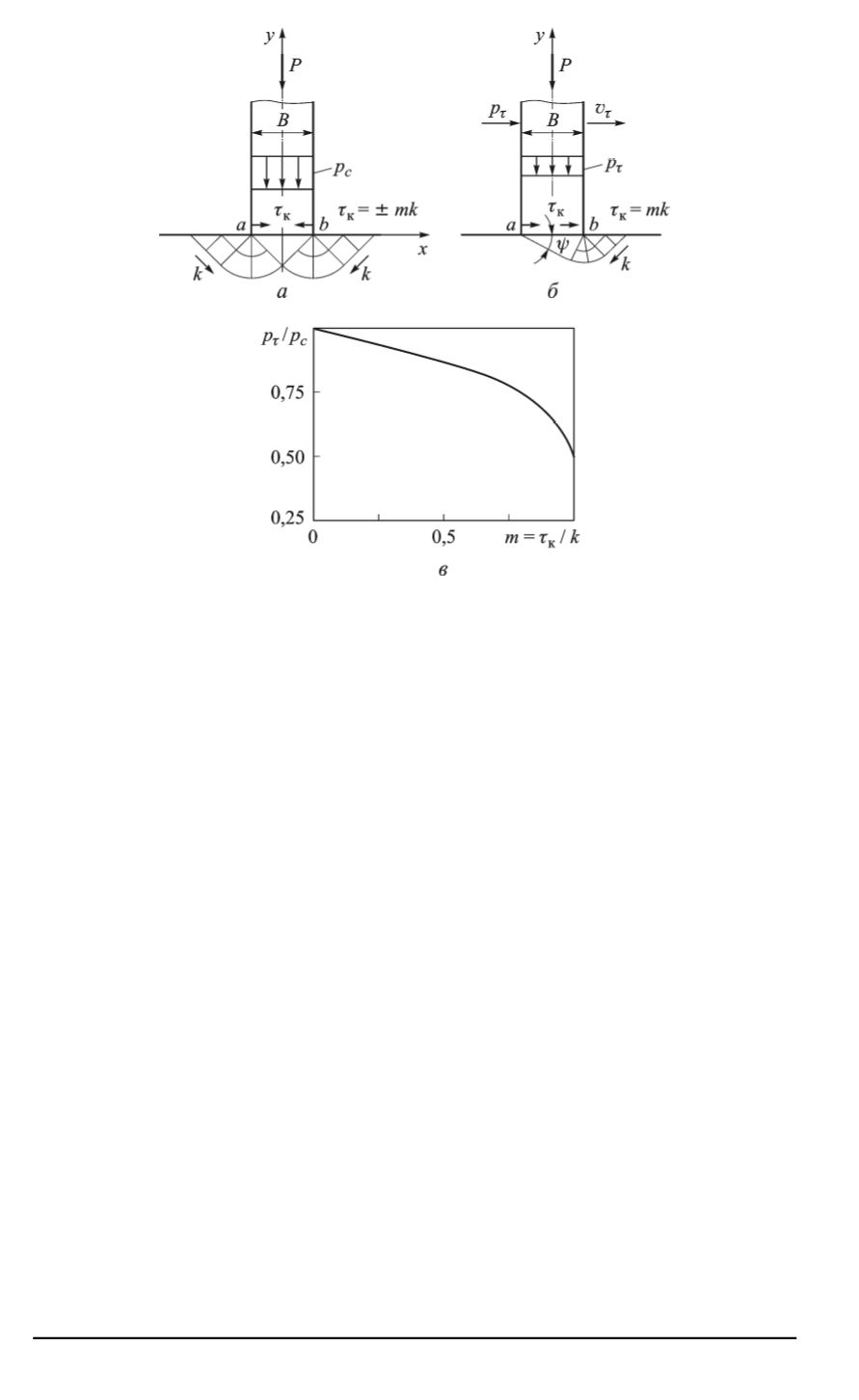
Рис. 1. Влияние контактного трения
τ
к
на предельные нормальные напряже-
ния:
а
— поле линий скольжений классического решения Прандтля;
б
— поле линий
скольжений при однонаправленных контактных касательных напряжениях
τ
к
;
в
—
график зависимости предельных нормальных напряжений
p
τ
/p
c
от
m
=
τ
к
/k
(базовым) результатом для расчета их контактной прочности служит
классическое решение Прандтля (рис. 1,
а
). Предельные контактные
давления
p
c
=
p
c
в решении Прандтля определяются по формуле
p
c
= 2
k
(1 +
π/
2) = 2
,
571
∙
2
k.
(1)
Формула Прандтля (1) определяет значение предельного контакт-
ного давления
p
c
=
p
c
при вдавливании плоского пуансона в одно-
родную идеально пластическую полуплоскость с
τ
max
=
k
=
const.
Решение Прандтля — это одно из наиболее востребованных решений
теории пластичности, и оно многократно проверялось эксперимен-
тально.
В работе [5] рассмотрен вопрос об определении нормальных пре-
дельных контактных напряжений
p
c
для контактируюших твердых тел
различной начальной формы. Показано, что при вдавливании в идеаль-
ное жесткопластическое полупространство цилиндрического пуансона
с плоской подошвой и произвольной выпуклой односвязной формой
контура в плане, предельные контактные напряжения
p
c
изменяются
в интервале [4]:
0
,
866
p
c
< p
c
≤
p
c
,
(2)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2012. № 4 101


