
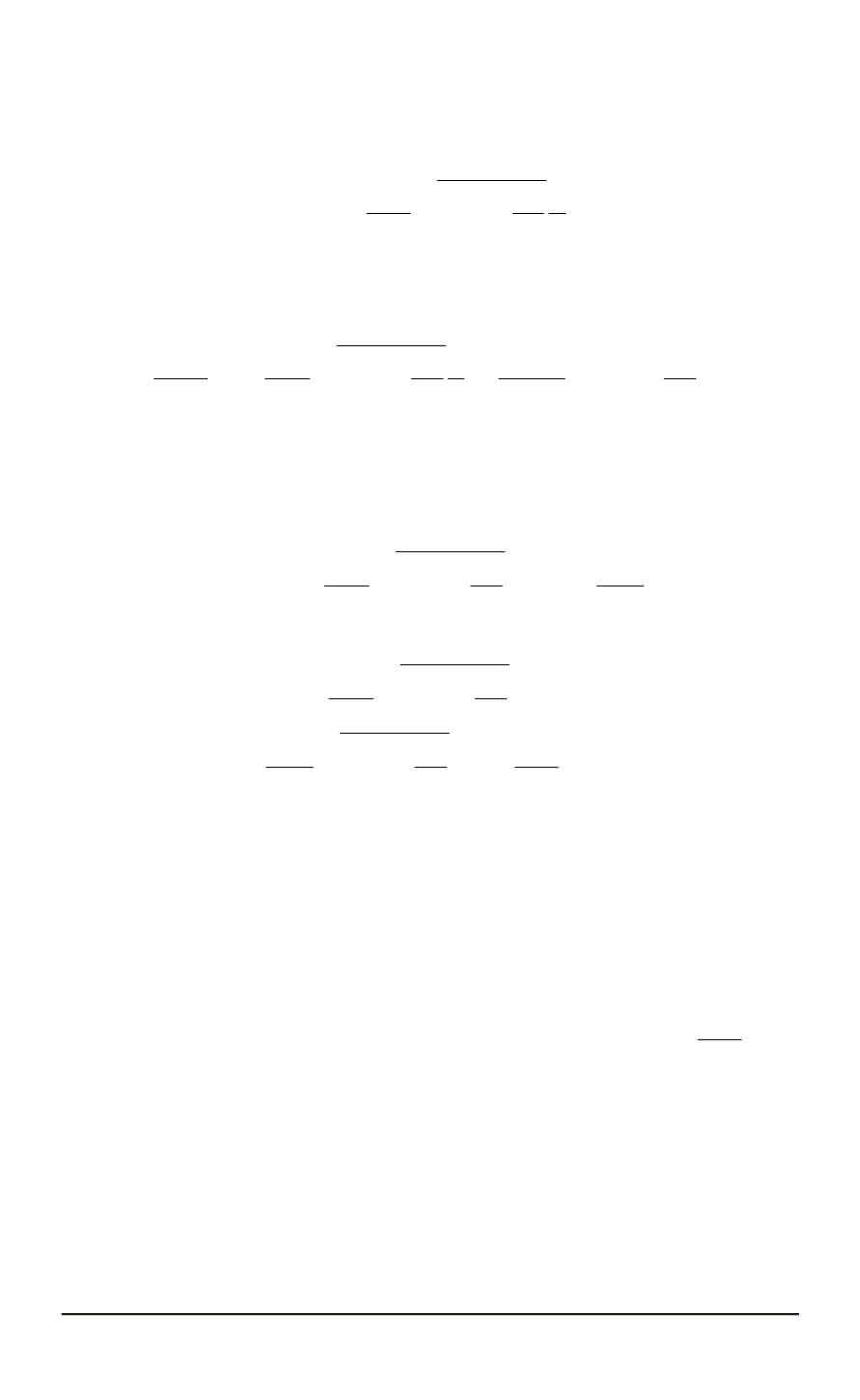
Значение постоянной
C
1
в формулах (27) находится из условия,
что для полосы конечных размеров точка, лежащая на пересечении
осей симметрии заготовки (
x
=
L/
2
;
y
= 0
) остается неподвижной в
процессе деформаций:
C
1
=
−
1
,
5
k
E
r
1
−
m
2
h
2
H
2
L
2
.
(29)
Значение постоянной
С
2
находится из условия, что горизонтальное
перемещение
u
непрерывно на линиях раздела
|
y
|
=
h/
2
упругой и
пластических областей:
С
2
=
3
mk
4
EH
h
2
−
1
,
5
k
E
r
1
−
m
2
h
2
H
2
L
2
+
1
,
5
kH
mE
1
−
m
2
h
2
H
2
.
(30)
Деформации в тонкой упругопластической полосе.
По известному
полю перемещений, определяемому формулами (27) и (28), значения
деформаций
ε
x
, ε
y
и
γ
xy
вычисляются по формулам (3)–(5).
В упругой области (
−
h/
2
≤
y
≤
h/
2
) —
ε
x
=
−
ε
y
=
1
,
5
k
E
r
1
−
m
2
h
2
H
2
;
γ
xy
=
6
mk
EH
y.
(31)
В пластических областях (
h/
2
≤ |
y
| ≤
H/
2
) —
ε
x
=
−
ε
y
=
1
,
5
k
E
r
1
−
m
2
h
2
H
2
;
γ
xy
=
6
mk
EH
r
1
−
m
2
h
2
H
2
1
−
4
m
2
H
2
y
2
−
0
,
5
y.
(32)
Деформированное состояние в упругопластической полосе опре-
деляется линейными деформациями
ε
x
=
−
ε
y
и деформациями сдви-
га
γ
xy
.
Первое деформированное состояние является результатом пласти-
ческого сжатия тонкой полосы между гладкими штампами (
m
= 0
),
второе — между шероховатыми штампами (
m >
0
). В первом слу-
чае пластические деформации возникают при
h
=
H
, что согласно
формулам (31) и (32) отвечает деформациям
ε
x
=
−
ε
y
=
1
,
5
k
E
. Это
же значение деформаций получаем из тех же формул при
h
= 0
или
m
= 0
. Это означает, что при отсутствии контактного трения начало
пластических деформаций при нагружении тонкой полосы совпадает
с моментом, когда она становится полностью пластичной. В этом слу-
чае в деформируемой тонкой полосе отсутствует этап одновременного
наличия в ней упругого и пластических участков.
На оси симметрии тонкой полосы, т.е. при
y
= 0
, согласно фор-
мулам (31) и (32) деформации сдвига
γ
xy
= 0
. Поэтому материальные
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 3 111

















