
Из решения Прандтля можно получить следующее выражение для
определения силы деформации
P
, приходящейся на единицу ширины
деформируемой полосы.
Обозначив
p
c
=
P/L
— среднее контактное давление,
L
— длина
контактной области, получим
p
c
=
mk
2
L
H
+
kC
a
.
(39)
Решение Прандтля справедливо только при достаточном удалении
от края и середины полосы. Это является следствием того, что гранич-
ные условия на краю полосы выполняются лишь в смысле принципа
Сен-Венана и это решение не применимо для центральной части за-
готовки, где происходит разветвление течения. Х. Гейрингер приняла,
что жесткий клин в центральной части деформируемой полосы, как
и в решении Прандтля, ограничен циклоидами. Это предположение
позволило ей рассчитать распределение скоростей в области центра
заготовки [3].
Работы многих исследователей позволили установить степень точ-
ности решения Прандтля при применении его к полосе конечных раз-
меров. Показано, что решение Прандтля, в указанном случае, носит ап-
проксимационный характер (рис. 4). В книге Р. Хилла [3] (при
m
= 1
)
показаны графики распределения нормального контактного давления
при пластическом сжатии тонкой полосы:
a
) согласно точному реше-
нию и
б
решению Прандтля. Из этого рисунка следует, насколько ре-
шение Прандтля представляет собой хорошее приближение к точному
решению.
Действительно, точное распределение контактного давления ко-
леблется около линейного распределения (39) Прандтля с постоянно
уменьшающейся амплитудой с ростом
L
. В задаче о сжатии полосы ко-
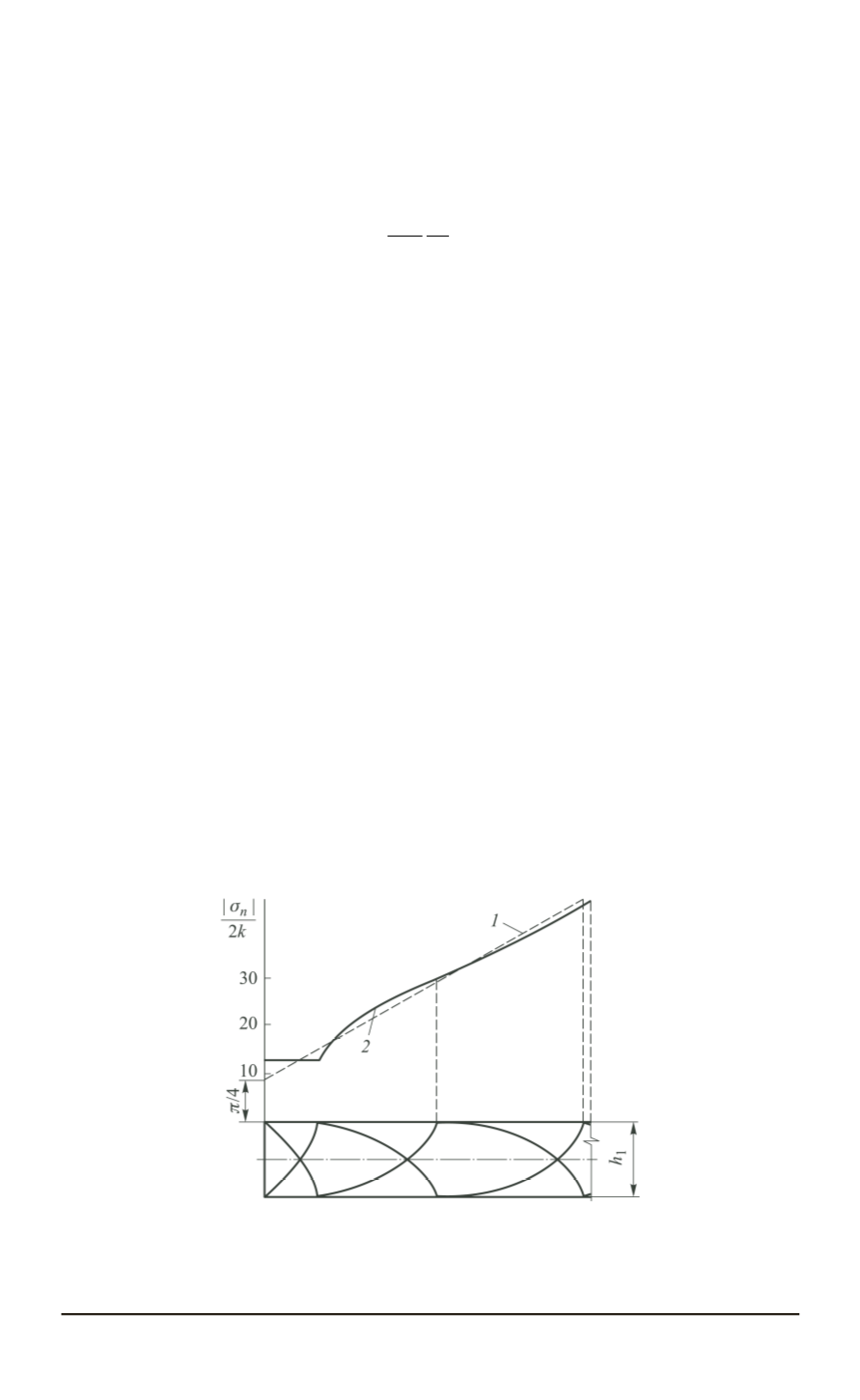
Рис. 4. Распределение нормального контактного давления при сжатии тонкой
пластической полосы в аппроксимационном решении Прандтля (
1
) и получае-
мое при построении поля линий скольжений (
2
) [3]
114 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 3

















