анта имеют следующий вид:
A
T
0
=
A
T
с
0
,
A
T
n
=
ber
(
p
n/
Fo
)
A
T
с
n
−
bei
(
p
n/
Fo
)
B
T
с
n
ber
2
(
p
n/
Fo
) +
bei
2
(
√
n
Fo
)
,
B
T
n
=
bei
(
p
n/
Fo
)
A
T
с
n
+
ber
(
p
n/
Fo
)
B
T
с
n
ber
2
(
p
n/
Fo
) +
bei
2
(
p
n/
Fo
)
.
Все рассуждения касающиеся средней температуры цилиндра и без-
размерного решения, аналогичны предыдущему частному случаю.
Результаты расчетов и их обсуждение.
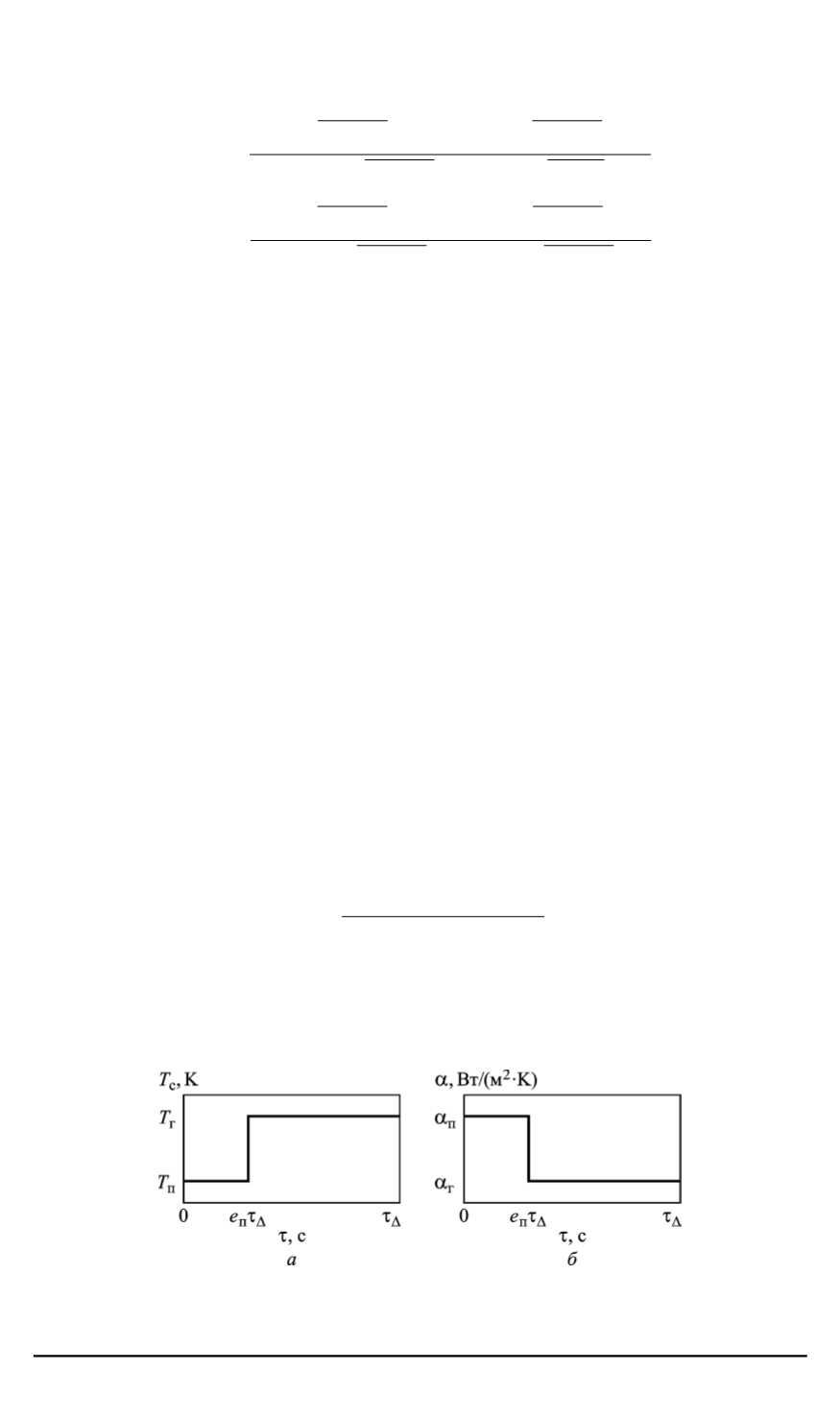
Для рабочего лопаточного
аппарата парциально охлаждаемой турбины будут характерны ступен-
чатые временные законы изменения температуры среды и коэффици-
ента теплоотдачи, показанные на рис. 1. Обе функции характеризуют-
ся степенью паровой парциальности
e
п
, определяющей длительность
охлаждения за период полного поворота ротора
τ
Δ
, и двумя значения-
ми зависимых величин —
T
п
,
T
г
и
α
п
,
α
г
соответственно. Здесь индекс
“п” относится к параметрам пара, а “г” — газа. Кроме того, коэф-
фициент теплоотдачи пара удобно выразить через соответствующую
величину для газа
α
п
=
βα
г
,
где коэффициент
β
≥
1
характеризует эффективность охлаждающего
агента. Для данных характеристик среды значение температуры
ˉ
T
с
вычисляется по формуле
ˉ
T
с
=
e
п
T
п
+ (1
−
e
п
)
T
г
,
а приближенная зависимость (25) для
ˉ
T
принимает вид
ˉ
T
≈
βe
п
T
п
+ (1
−
e
п
)
T
г
1 + (
β
−
1)
e
п
.
Расчет был проведен для цилиндра
R
= 0
,
015
м из жаропрочно-
го сплава ХН80ТБЮ с теплофизическими свойствами
a
= 7
,
225
×
×
10
−
6
м
2
/с;
λ
= 27
Вт/(м
∙
K), взятыми из справочника [14], и сле-
Рис. 1. Зависимость температуры среды (
а
) и коэффициента теплоотдачи (
б
) от
времени
64 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2011. № 4


