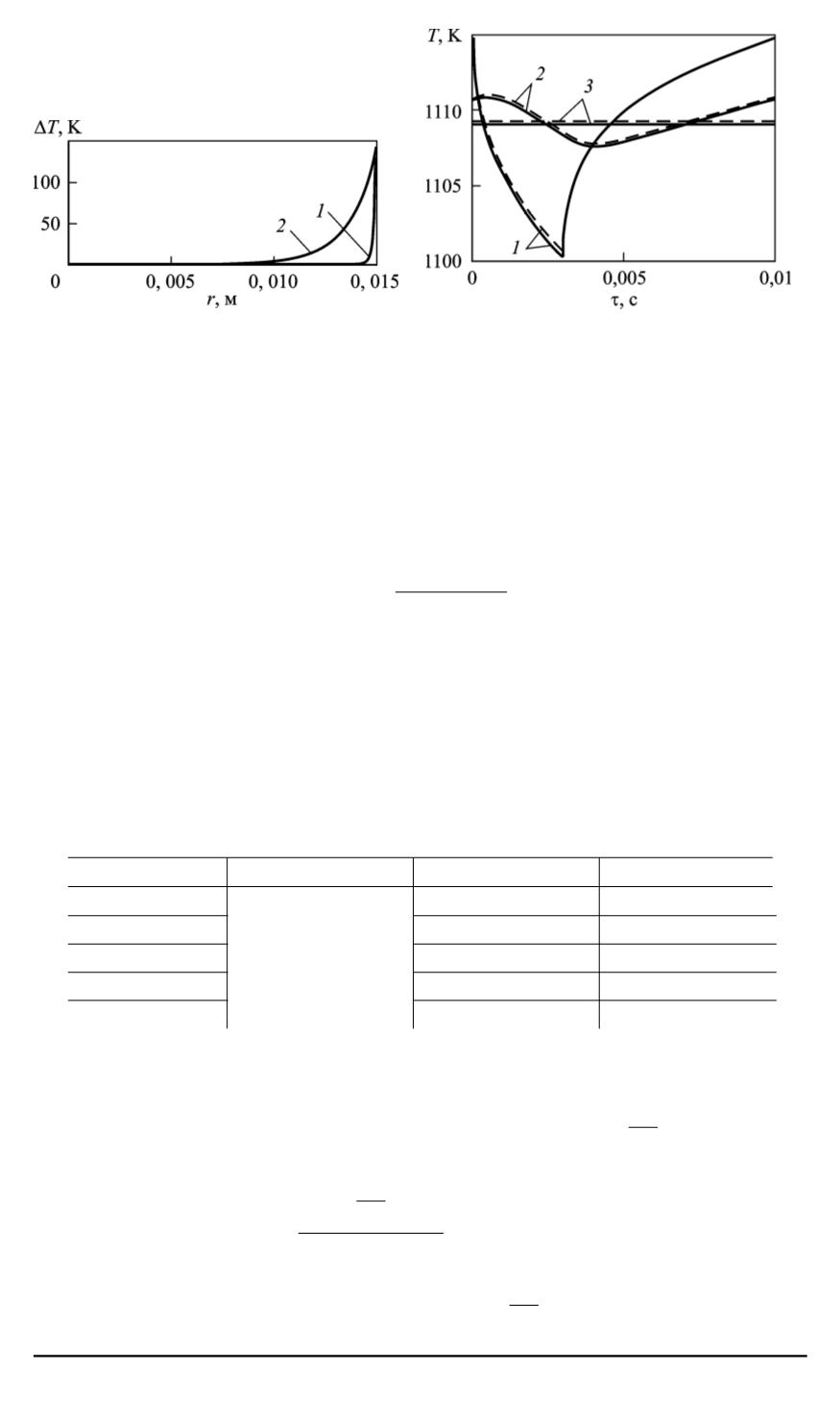
Рис. 3. Зависимость размаха коле-
баний температуры цилиндра от
радиуса для
τ
Δ
= 0
,
01
с (
1
) (масштаб
по оси
Δ
T
10:1) и 1 с (
2
)
Рис. 4. Зависимость температуры ци-
линдра от времени для периода ци-
кла 0,01 с на радиусах:
1
— 0,015 м;
2
— 0,0148 м;
3
— 0 м (штри-
ховая линия — аналитическое решение;
сплошная — численный расчет)
Интересно также оценить погрешность, которую дает формула (25)
для средней температуры цилиндра. Ее целесообразно искать в следу-
ющем виде:
Δ
T
=
ˉ
T
т.р
−
ˉ
T
п.р
ˉ
T
с
−
ˉ
T
п.р
,
где
ˉ
T
т.р
и
ˉ
T
п.р
— значения точного и приближенного расчетов
ˉ
T
. Ре-
зультаты вычислений сведены в таблицу, из которой следует, что при-
ближенное значение
ˉ
T
удовлетворительно согласуется с точными зна-
чениями для относительно больших периодов колебаний, а для малых
практически совпадает.
Сравнение результатов точных вычислений средней температуры
цилиндра за период с расчетом по приближенной формуле
τ
Δ
, c
ˉ
T
п.р
, K
ˉ
T
т.р
, K
Δ
T
, %
0,01
1109,26
0,62
0,1
1110,47
1,95
1
1108,70
1114,27
6,11
10
1125,74
18,67
100
1159,08
55,18
При переходе к безразмерным величинам характеристики среды
примут вид, показанный на рис. 5. Причем безразмерная избыточная
температура характеризуется только степенью паровой парциальности
e
п
, а критерий Био — еще своим средним значением Bi и коэффици-
ентом
β
. Критерии Био по газу и пару вычисляются по формулам:
Bi
г
=
Bi
1 + (
β
−
1)
e
п
,
Bi
п
=
β
Bi
г
.
Поведение функции безразмерной избыточной температуры в нашем
случае определяется параметрами Fo ,
e
п
, Bi,
β
.
66 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2011. № 4


