В этом случае накопленная деформация в точке А
(
см
.
рис
. 4),
на
-
чальная координата которой
z
0
=
h
0
/
2
,
e
i
A
= 2 ln
h
0
h
.
(43)
Накопленная деформация в точке О
,
начальная координата которой
z
0
= 0
,
e
i
O
= 0
.
(44)
3.
Затрудненное течение
(
µ
= 0
,
25
):
заготовка получает в процессе
деформации среднюю бочкообразность
,
так как радиальная скорость
v
ρ
на поверхностях контакта с инструментом имеет меньшую величи
-
ну
,
чем в срединной плоскости
.
Этот случай является промежуточным
между вариантами
1
и
2
,
и
,
следовательно
,
можно принять
a
= 0
,
5
,
b
= 0
,
5
.
Дальнейшее определение деформированного состояния в этом
случае осуществляется аналогично рассмотренным ранее
.
Но так как
функция
v
z
достаточно сложна
(
см
.
первое выражение системы
(29)),
то
в этом случае для определения зависимости между текущей и началь
-
ной координатами
z
=
f
(
z
0
)
приходится решать дифференциальное
уравнение Бернулли
,
что довольно трудоемко
.
Общие выражения для
текущей координаты и накопленной деформации аналогичны выведен
-
ным выражениям для случая затрудненного течения при выдавливании
стаканов
(
см
.
формулы
(3.98), (3.99)
в книге
[1]).
Поэтому приведем без
вывода окончательные результаты
:
e
i
A
= 1
,
5 ln
h
0
h
;
(45)
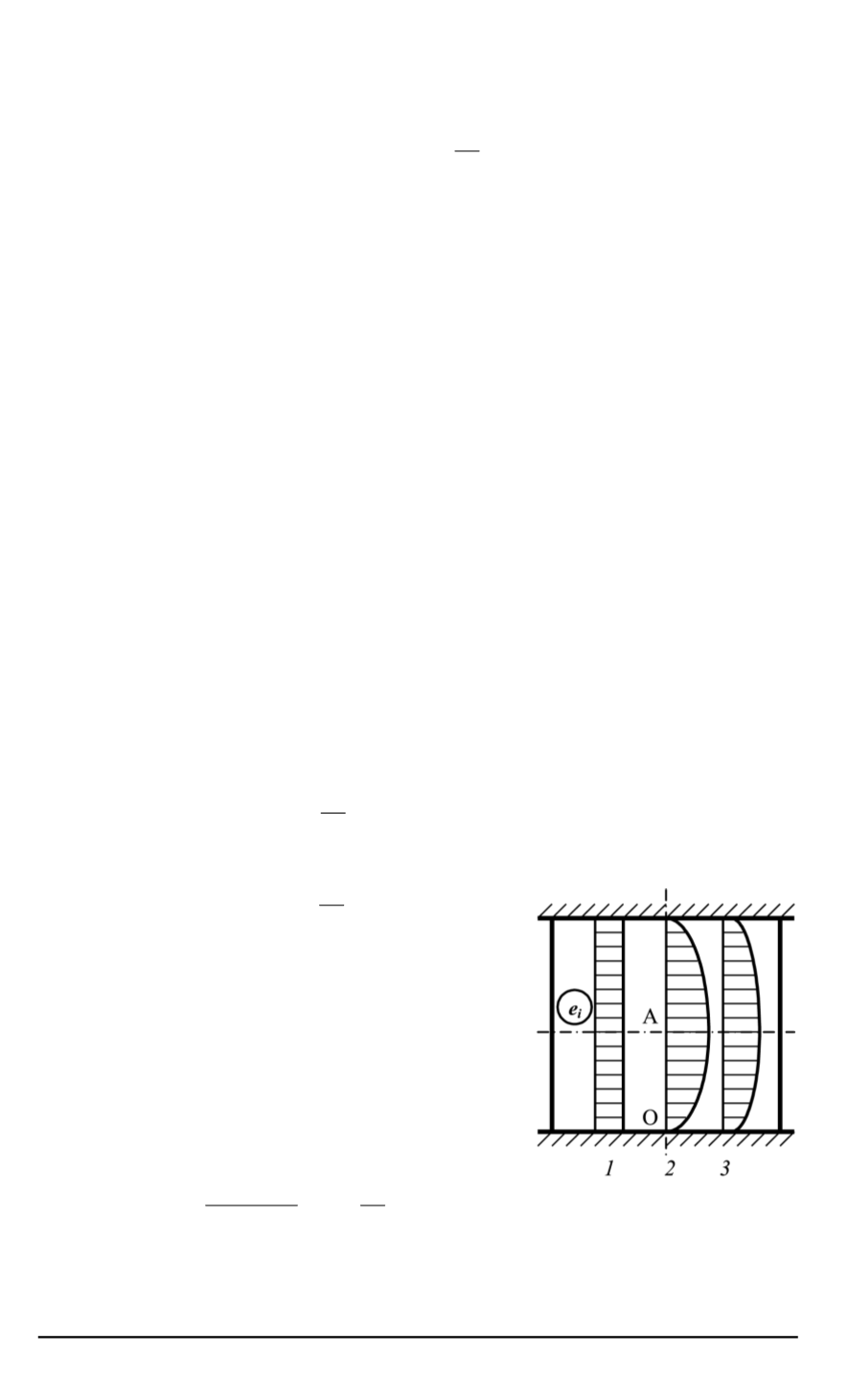
Рис
. 5.
Варианты распреде
-
ления накопленных дефор
-
маций по высоте осаживае
-
мой заготовки
e
i
O
= 0
,
5 ln
h
0
h
.
(46)
Соответствующие рассмотренным слу
-
чаям эпюры распределения накопленных
деформаций по высоте осаживаемой заго
-
товки показаны на рис
. 5.
С достаточной
для практики точностью можно считать
,
что
средняя величина накопленной деформации
в объеме заготовки определяется выраже
-
нием
e
i
=
e
i
A
+
e
i
O
2
= ln
h
0
h
,
(47)
т
.
е
.
будет одинакова во всех трех случаях
.
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2004.
№
1 91


