С учетом продольных касательных сил
q
t
полный вектор контакт-
ной нагрузки
~q
принимает вид
~q
=
q
n
~n
+
q
t
~t ,
где вектор
~t
касательной к недеформируемой опорной поверхности
образован как
[
~n, ~i
]
и направлен в сторону движения опорной по-
верхности.
Обозначим радиусы-векторы текущих точек протектора и брекера
как
~r
v
и
~r
u
соответственно; угловую координату точек брекера —
ϕ
.
Также введем угловую скорость
Ω
стационарного качения; скорость
движения основания
V
.
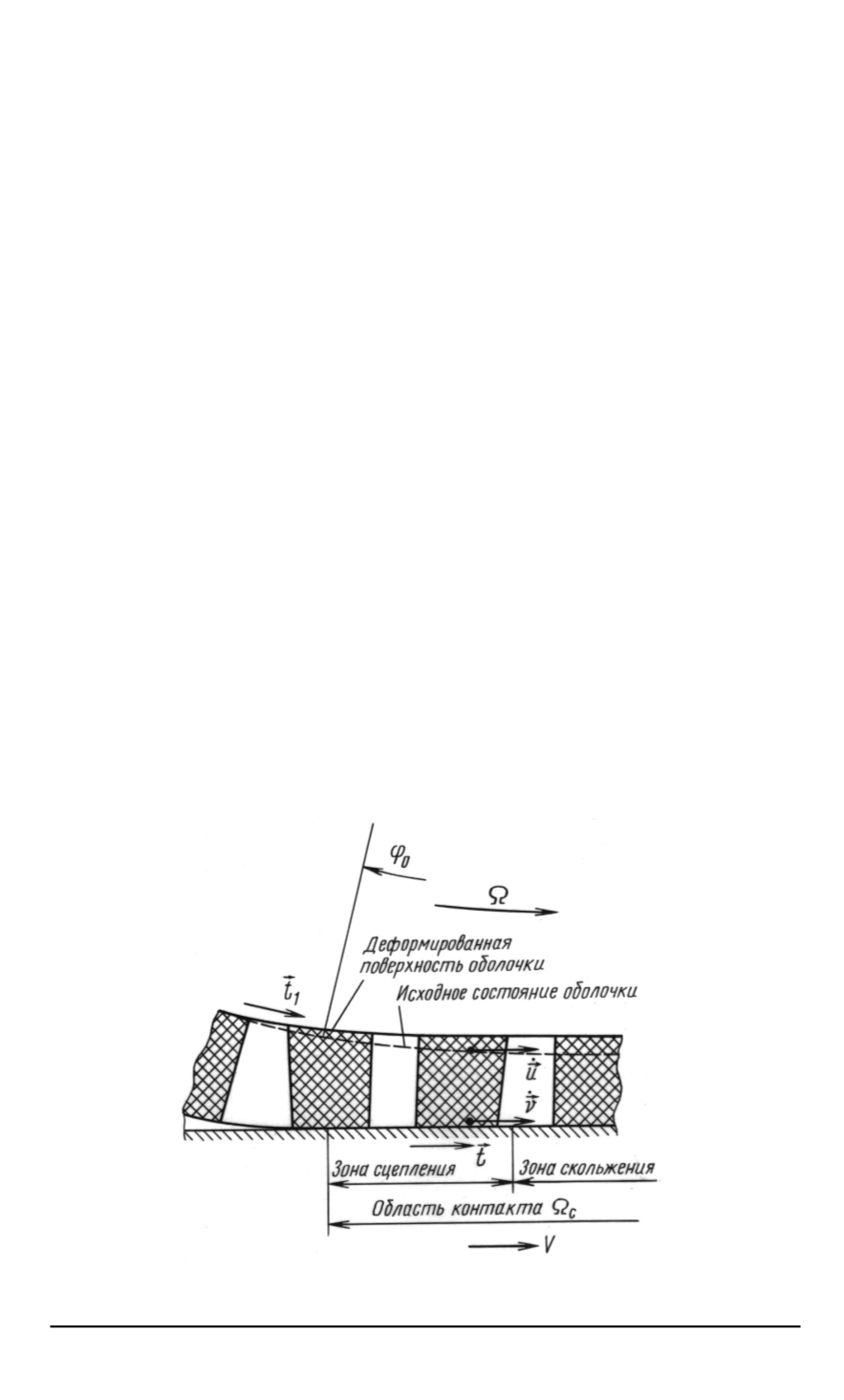
Для определения касательных сил в месте контакта используем
концепцию “сцепление–скольжение” [1], [11], согласно которой пло-
щадка контакта делится на зону сцепления и зону скольжения (рис. 6).
Тангенциальная составляющая контактной нагрузки определяется
по модели сухого (кулонова) трения, представляемой неравенством
|
q
t
|
6
μq
n
,
(15)
где
μ
— коэффициент трения продольного скольжения шашки протек-
тора по опорной поверхности.
Деформации сдвига элементов протектора и касательные напряже-
ния возникают из-за различия скоростей
˙
~r
v
,
˙
~r
u
, с которыми движутся в
пятне контакта точки протектора и соответствующие им точки бреке-
Рис. 6. Схема определения сдвигов элемента протектора при стационарном ка-
чении
28 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 1


