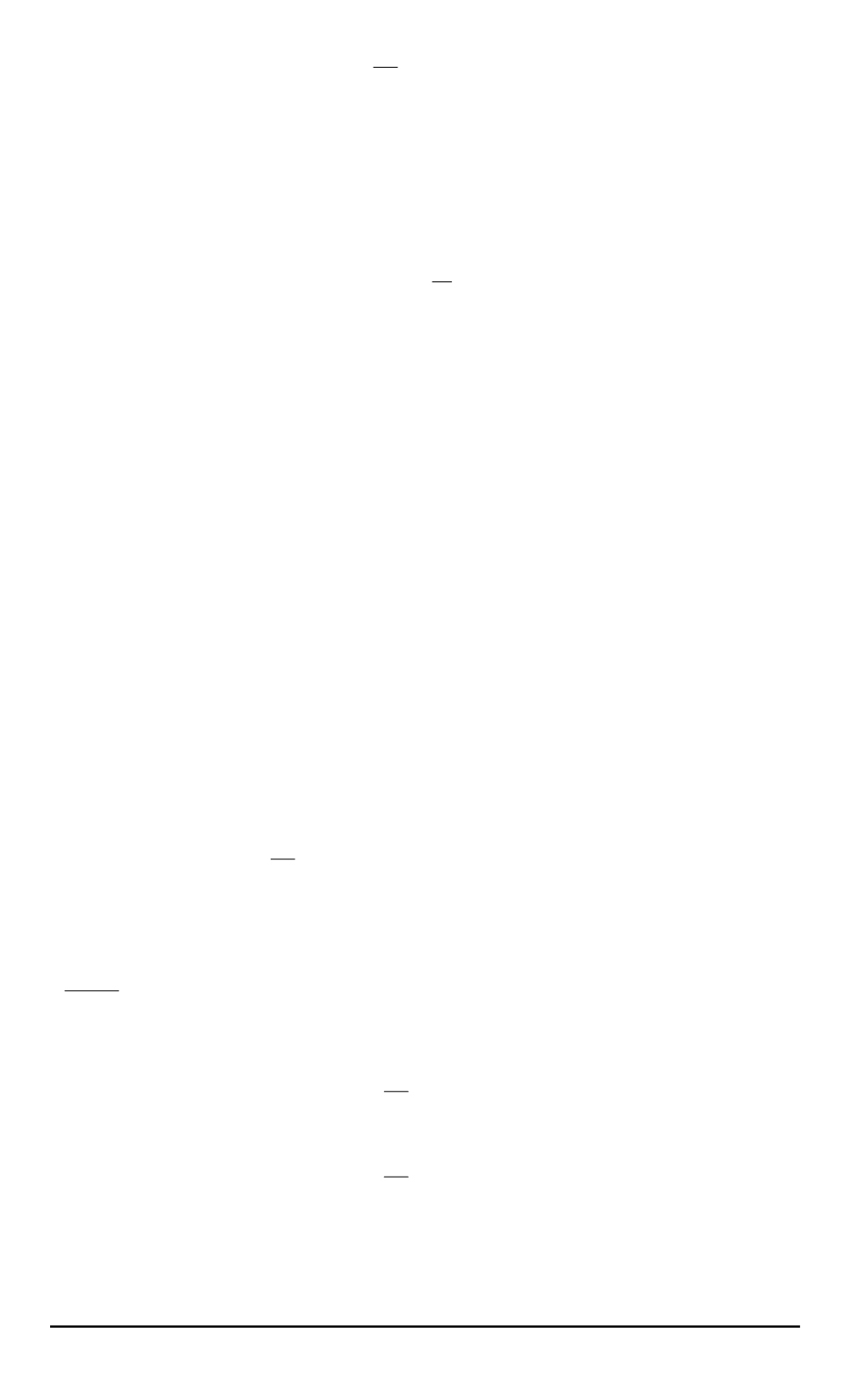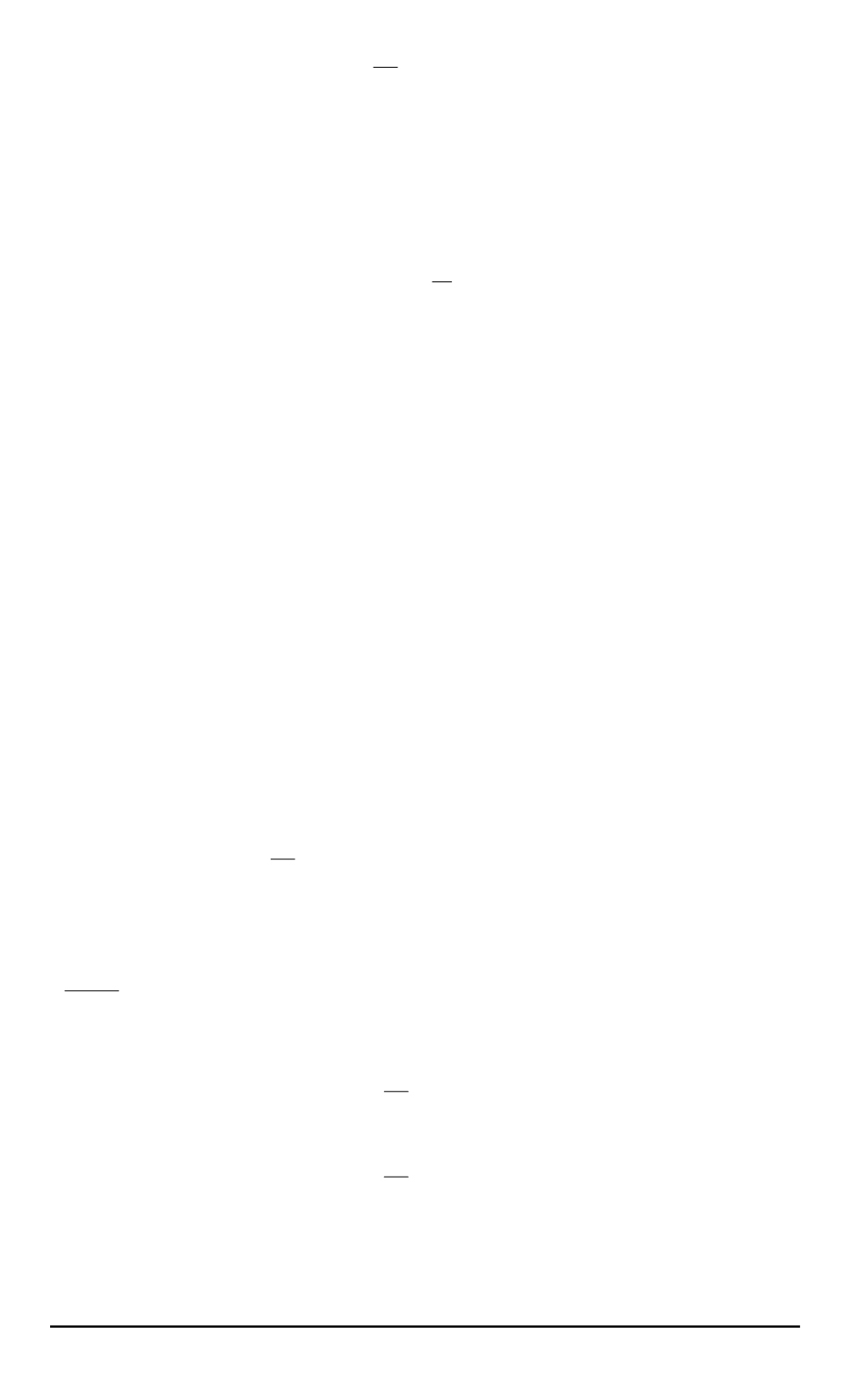
δ
Π
сц
=
ZZ
Ω
сц
G
h
p
(
u
t
−
g
0
t
)
δu
t
d
Ω
.
В зоне скольжения скорость точек протектора отличается от ско-
рости движения основания и является неизвестной. В этой зоне угол
сдвига протектора принимается равным максимально возможному из
условия ограничения тангенциальных сил в контакте (15):
γ
ск
p
=
μ
G
q
n
.
Будем считать, что при скольжении шашки протектора перемеща-
ются вместе с оболочкой шины в направлении
~t
без дополнительного
деформирования. Таким образом, тангенциальные силы
q
t
, совершаю-
щие работу на возможных перемещениях
δu
t
, зависят от нормальных
сил
q
n
и, следовательно, от нормальных перемещений
u
n
, однако не
зависят от тангенциальных перемещений. Поэтому виртуальная рабо-
та тангенциальных сил на бесконечно малых перемещениях
δ~u
будет
равна
δA
ск
=
−
ZZ
Ω
ск
μq
n
δ~v
∙
~t d
Ω =
−
ZZ
Ω
ск
μq
n
δu
t
d
Ω
.
Добавляя энергию сдвига протектора к функционалу потенциаль-
ной энергии системы (7), получаем следующее вариационное уравне-
ние:
δ
Π
mod
=
δ
Π +
ZZ
Ω
c
k
p
(
u
n
−
g
0
)
δu
n
d
Ω+
+
ZZ
Ω
сц
G
h
p
(
u
t
−
g
0
t
)
δu
t
d
Ω +
ZZ
Ω
ск
μk
p
(
u
n
−
g
0
)
δu
t
d
Ω = 0
.
Это уравнение может быть записано в матричной форме:
∂
Π
∂
{
f
}
+ ([
K
c
] + [
K
сц
] + [
K
ск
])
{
f
} −
(
{
F
c
}
+
{
F
сц
}
+
{
F
ск
}
) = 0
,
(17)
где
[
K
сц
] =
ZZ
Ω
сц
G
h
p
[
N
]
T
{
t
}{
t
}
T
[
N
]
d
Ω;
{
F
сц
}
=
ZZ
Ω
сц
G
h
p
g
0
t
[
N
]
T
{
t
}
d
Ω;
[
K
ск
] =
ZZ
Ω
ск
μk
p
[
N
]
T
{
t
}{
n
}
T
[
N
]
d
Ω;
30 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 1