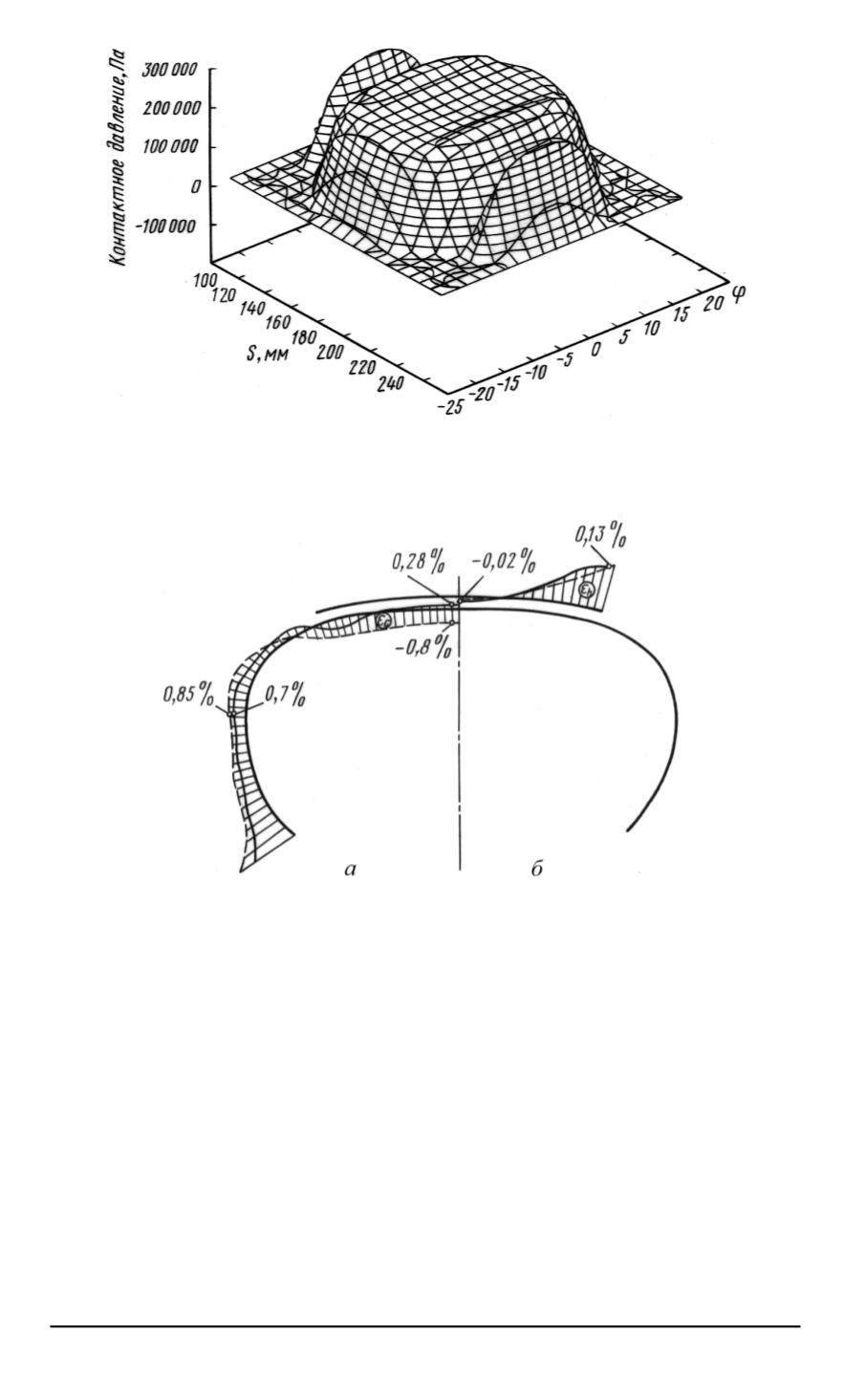
Рис. 4. Распределение контактного давления при обжатии на плоскость силой
Q
z
= 3700
Н
Рис. 5. Сопоставление результатов решения задачи обжатия. Эпюра деформа-
ций корда в каркасе (
а
) и брекере (
б
) (масштабы эпюр различны):
сплошные линии — решение геометрически нелинейной задачи МКЭ; штриховые —
решение задачи в дифференциальной линеаризованной постановке
Контактная задача при действии тягово-тормозных сил.
При
решении контактной задачи качения шины алгоритм, изложенный в
предыдущем параграфе, должен быть дополнен учетом касательных
сил в площади контакта.
Рассмотрим качение шины с малой скоростью, при которой можно
пренебречь силами инерции. В случае большой скорости силы инер-
ции вводятся в систему, например, по схеме, описанной в работе [2].
При формулировании задачи будем считать, что ось колеса неподвиж-
на, движется опорная поверхность, являющаяся либо плоскостью, ли-
бо цилиндрической поверхностью бегового барабана.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 1 27


