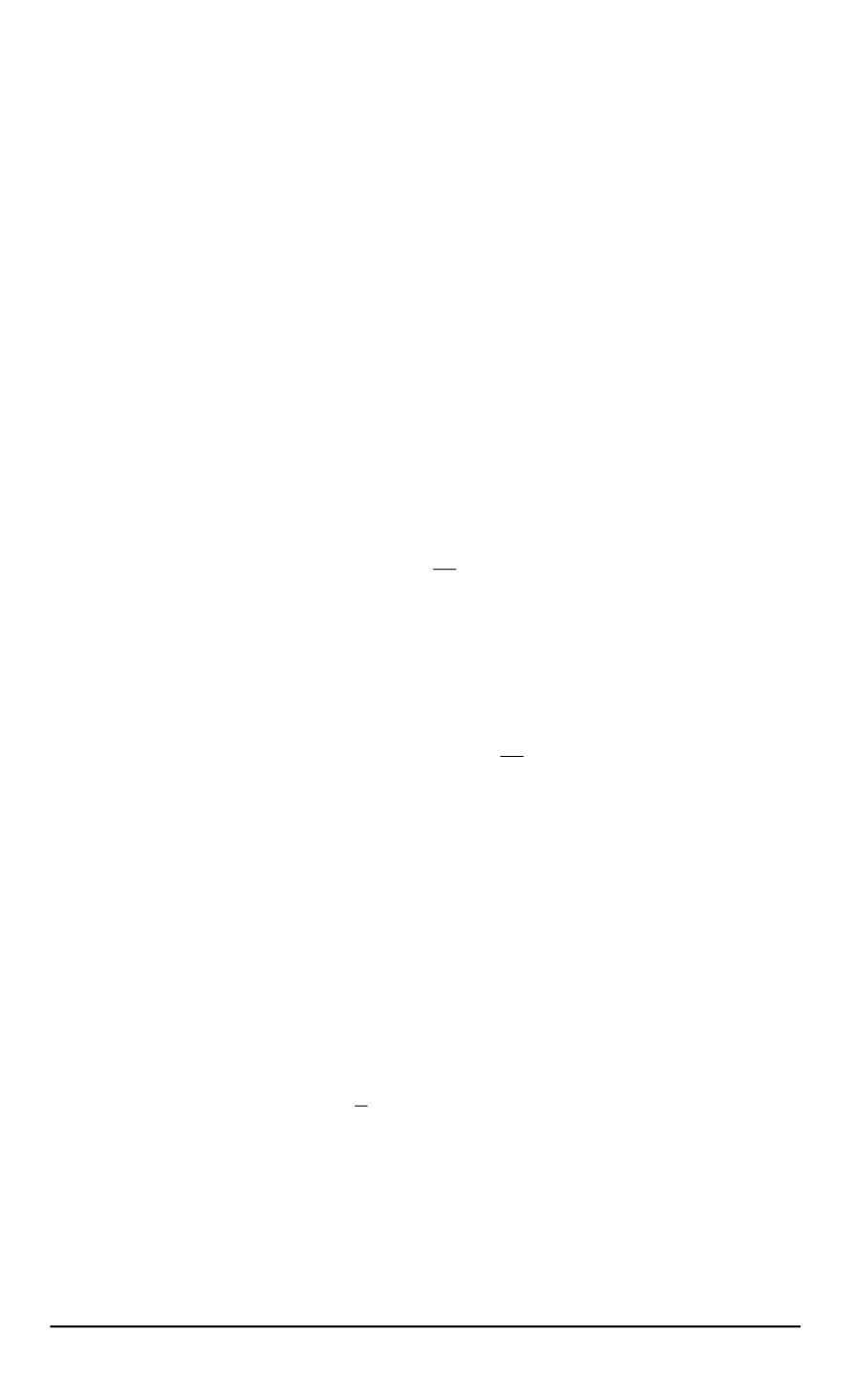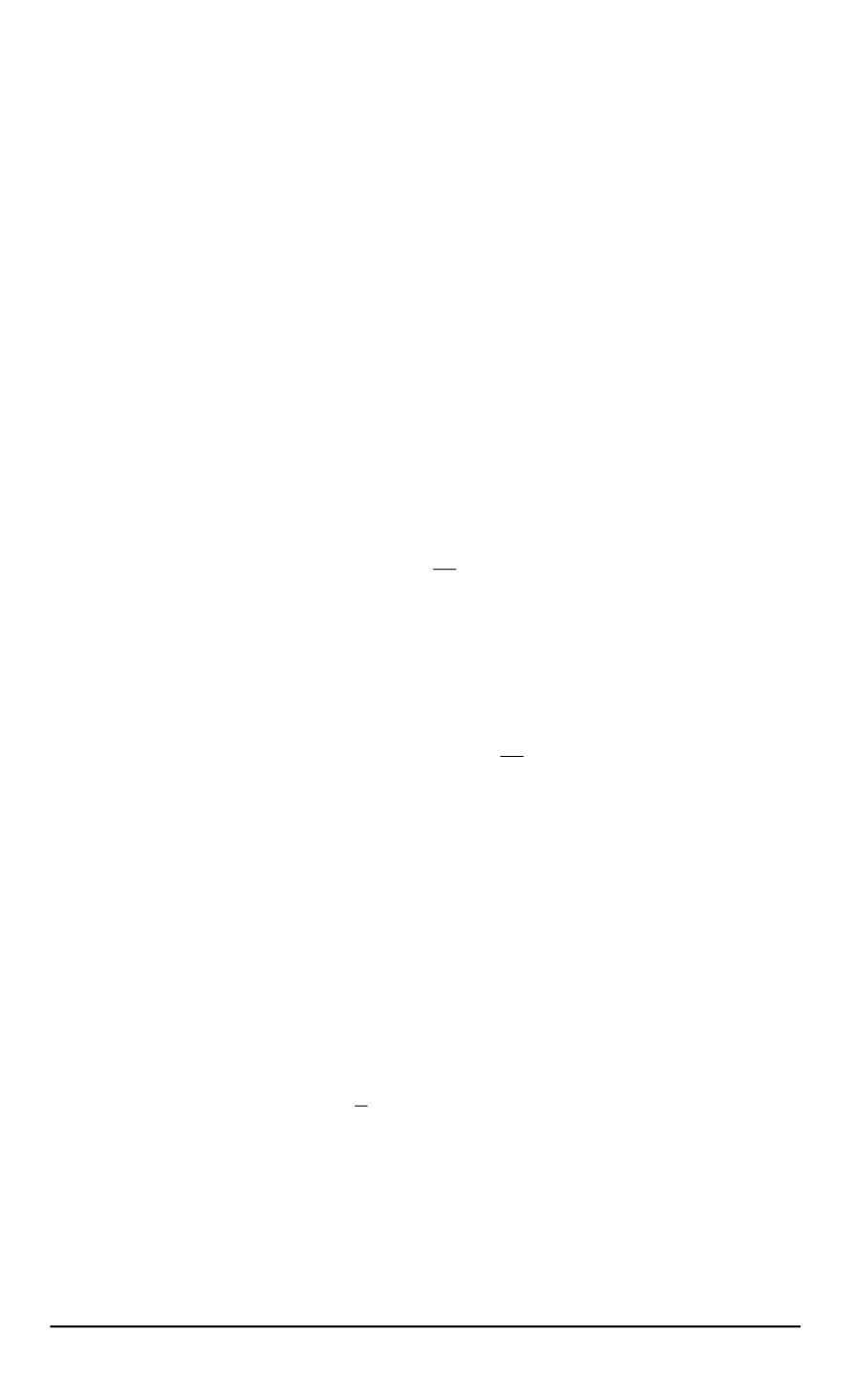
— тангенсы углов наклона касательных к опорной поверхности.
Для пологой поверхности величины
ψ
0
x
,
ψ
0
y
в пределах контакта
являются малыми, поэтому будем пренебрегать их квадратами и про-
изведениями по сравнению с единицей. С этой точностью определим
единичный вектор внешней нормали к опорной поверхности как
~n
=
−
ψ
0
x
~i
−
ψ
0
y
~j
+
~k
и представим функцию внедрения (1) в виде
g
=
g
0
−
(
~n, ~v
)
,
(2)
где
~v
=
v
x
∙
~i
+
v
y
∙
~j
+
v
z
∙
~k
.
Перемещения точек наружной поверхности протектора складыва-
ются из перемещений корпуса шины (оболочки)
~u
и относительных
перемещений
Δ
~h
, связанных с обжатием протектора:
~v
=
~u
+ Δ
~h .
(3)
Рассматривая протектор как изотропный винклеровский слой, пола-
гаем
Δ
~h
=
q
n
k
p
~n ,
(4)
где
q
n
>
0
— нормальное контактное давление;
k
p
— жесткость про-
тектора.
Из соотношений (2)–(4) следует связь между контактным давлени-
ем и функцией внедрения:
g
=
g
0
−
(
~n, ~u
)
−
q
n
k
p
.
Контактное давление должно быть найдено так, чтобы внедрение
обратилось в ноль. Таким образом,
q
n
=
(
k
p
(
g
0
−
(
~n, ~u
))
,
если
g
0
−
(
~n, ~u
)
>
0;
0
,
если
g
0
−
(
~n, ~u
)
6
0
.
(5)
Область контакта
Ω
c
характеризуется неравенством
g
0
−
(
~n, ~u
)
>
0
.
Для решения контактной задачи модифицируем функционал пол-
ной потенциальной энергии оболочки, моделирующей шину, путем
добавления к нему энергии обжатия протектора:
Π
mod
= Π +
1
2
ZZ
Ω
c
k
p
g
0
−
(
~n, ~u
)
2
d
Ω
.
(6)
Исходя из принципа стационарности функционала (6), получаем
вариационное уравнение
δ
Π
mod
=
δ
Π +
ZZ
Ω
c
k
p
(
~n, ~u
) (
~n, δ~u
)
−
g
0
(
~n, δ~u
)
d
Ω = 0
,
(7)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 1 23