
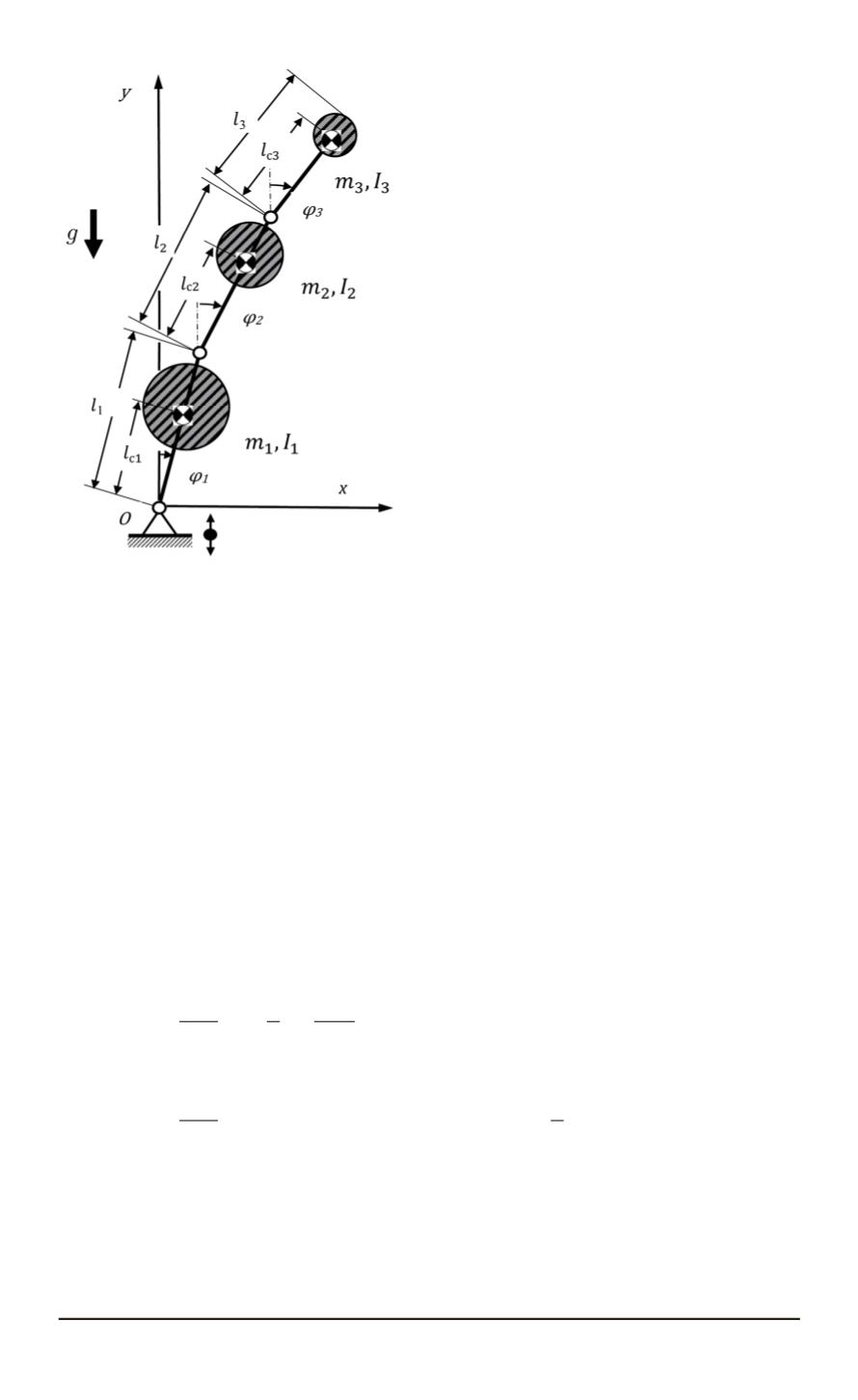
Рис. 4. Расчетная схема тройного ма-
ятника
Уравнения движения маятни-
ка и численное решение зада-
чи устойчивости параметриче-
ски стабилизируемого обращен-
ного тройного маятника.
В на-
стоящей работе задача устойчи-
вости решается численно и экс-
периментально. Поэтому большое
значение имеет выбор математи-
ческой модели объекта исследова-
ния (параметров маятника и фор-
мы представления уравнений дви-
жения). От принятой математиче-
ской модели зависит качество и
удобство использования расчетных
и экспериментальных результатов,
а также общность полученных ре-
зультатов и выводов. Рассмотрим
возможные формы записи линей-
ных уравнений движения маятни-
ковых систем с параметрическим
возбуждением, с целью выбрать наиболее рациональный для данного
исследования формат.
Начнем сравнительный анализ с простейшей системы — однозвен-
ного математического маятника с идеальными связями при моногар-
моническом перемещении точки подвеса по вертикали с амплитудой
A
и частотой
p
. Математической моделью объекта в этом случае являет-
ся уравнение Матье [13, 14] или канонические уравнения (уравнения
Гамильтона) [15].
В литературе используется один из двух вариантов записи уравне-
ния Матье. Первый вариант — уравнения с размерными параметрами
и размерным временем
d
2
ϕ
dt
2
+
g
l
−
Ap
2
l
cos
pt ϕ
= 0
,
или
d
2
ϕ
dt
2
+
p
2
1
(1
−
μ
cos
pt
)
ϕ
= 0
, p
2
1
=
g
l
;
t, ϕ
∈
R
,
(1)
где
ϕ
— отклонение маятника от вертикали;
t
— время;
p
1
— собствен-
ная частота прямого маятника;
р
— частота параметрического возбу-
ждения;
μ
= (
Ap
2
)
/g
— глубина модуляции собственной частоты;
l
—
длина маятника;
А
— амплитуда параметрического возбуждения. Фор-
ма (1) получила в нашей стране широкое распространение благодаря
40 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 6
















