
dϕ
2
dt
= A(
t
)
ϕ
2
, t
∈
R
, ϕ
2
(
t
)
∈
R
2
N
.
(11)
Здесь
ϕ
2
=
{
ϕ
1
, ϕ
2
, . . . , ϕ
N
,
˙
ϕ
1
, . . . ,
˙
ϕ
2
N
}
— вектор фазовых пере-
менных размерности
2
N
;
A(
t
)
— действительная квадратная
T
-
периодическая матрица коэффициентов порядка
2
N
×
2
N
, выражаемая
через инерционную матрицу
M
, матрицу квазижесткости
C(
t
)
(10) и
единичную матрицу
E
A(
t
) =
0
E
−
M
−
1
C(
t
) 0
.
Уравнение (11) является уравнением в возмущениях с тривиальным
решением
ϕ
2
= 0
, соответствующим невозмущенному (вертикально-
му) положению маятника.
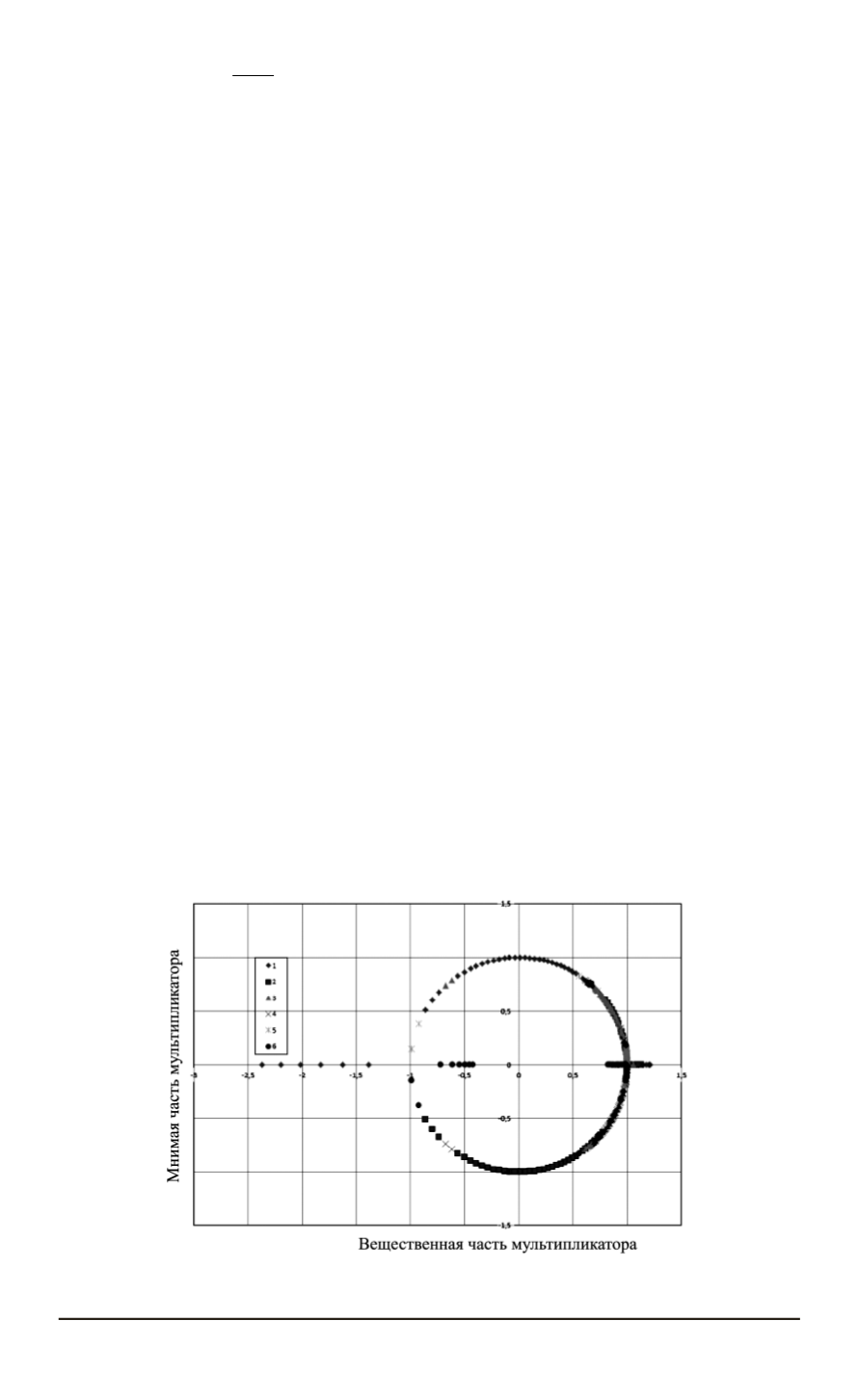
Для уравнения (11) в соответствии с теорией Флоке вычисляет-
ся матрица монодромии и мультипликаторы. Пример эволюции шести
мультипликаторов при изменении параметров возбуждения показан на
рис. 5. Затем, следуя теоремам Н.Г. Четаева [23] по поведению муль-
типликаторов на комплексной плоскости, решается вопрос об устой-
чивости тривиального решения (11).
Методика экспериментального определения границ области
устойчивости.
Экспериментальная область устойчивости тройного
обращенного маятника получена на установке и возбудителе вибрации
(рис. 6), созданных специально для выполнения настоящей работы.
С использованием экспериментальной установки определены гра-
ничные значения параметров возбуждения (амплитуды и частоты, ле-
жащие на границе области устойчивости).
Последовательность действий при определении граничных значе-
ний следующая. Сначала задается амплитуда параметрического возбу-
ждения. Для каждой установленной на вибраторе амплитуды колеба-
ний осуществляется проход по частоте снизу вверх в рассматриваемом
Рис. 5. Пример эволюции мультипликаторов на комплексной плоскости
44 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 6
















