
ε
x
=
∂u/∂x
;
(3)
ε
y
=
∂v/∂y
;
(4)
γ
xy
=
∂u/∂y
+
∂v/∂x
(5)
— тремя уравнениями деформаций, и для упругого тела — тремя урав-
нениями, связывающими напряжения и деформации (закон Гука), ко-
торые записываются как [1]
∂u/∂x
=
1
−
ν
2
E
σ
x
−
ν
1
−
ν
σ
y
;
(6)
∂v/∂y
=
1
−
ν
2
E
σ
y
−
ν
1
−
ν
σ
x
;
(7)
∂u/∂y
+
∂v/∂x
=
2(1 +
ν
)
E
τ
xy
.
(8)
В уравнениях (1)–(8):
σ
x
,
σ
y
— нормальные напряжения ;
τ
xy
—
касательное напряжение;
u
и
v
— перемещения по осям
x
и
y
;
ν
—
коэффициент Пуассона;
E
— модуль упругости.
Диаграмма зависимости интенсивности напряжений
σ
i
от интен-
сивности деформаций
ε
i
для упругого идеально пластичного матери-
ала показана на рис. 1;
σ
s
— предел текучести материала.
Из исходной системы уравнений (1)–(8) получаем систему из четы-
рех уравнений (1), (2), (9) и (10) с четырьмя неизвестными
σ
x
, σ
y
, τ
xy
, v
:
∂v
∂y
=
1
−
ν
2
E
σ
y
−
ν
1
−
ν
σ
x
;
(9)
2 (1 +
ν
)
E
∂τ
xy
∂x
=
1
−
ν
2
E
∂σ
x
∂y
−
ν
1
−
ν
∂σ
y
∂y
+
∂
2
v
∂x
2
.
(10)
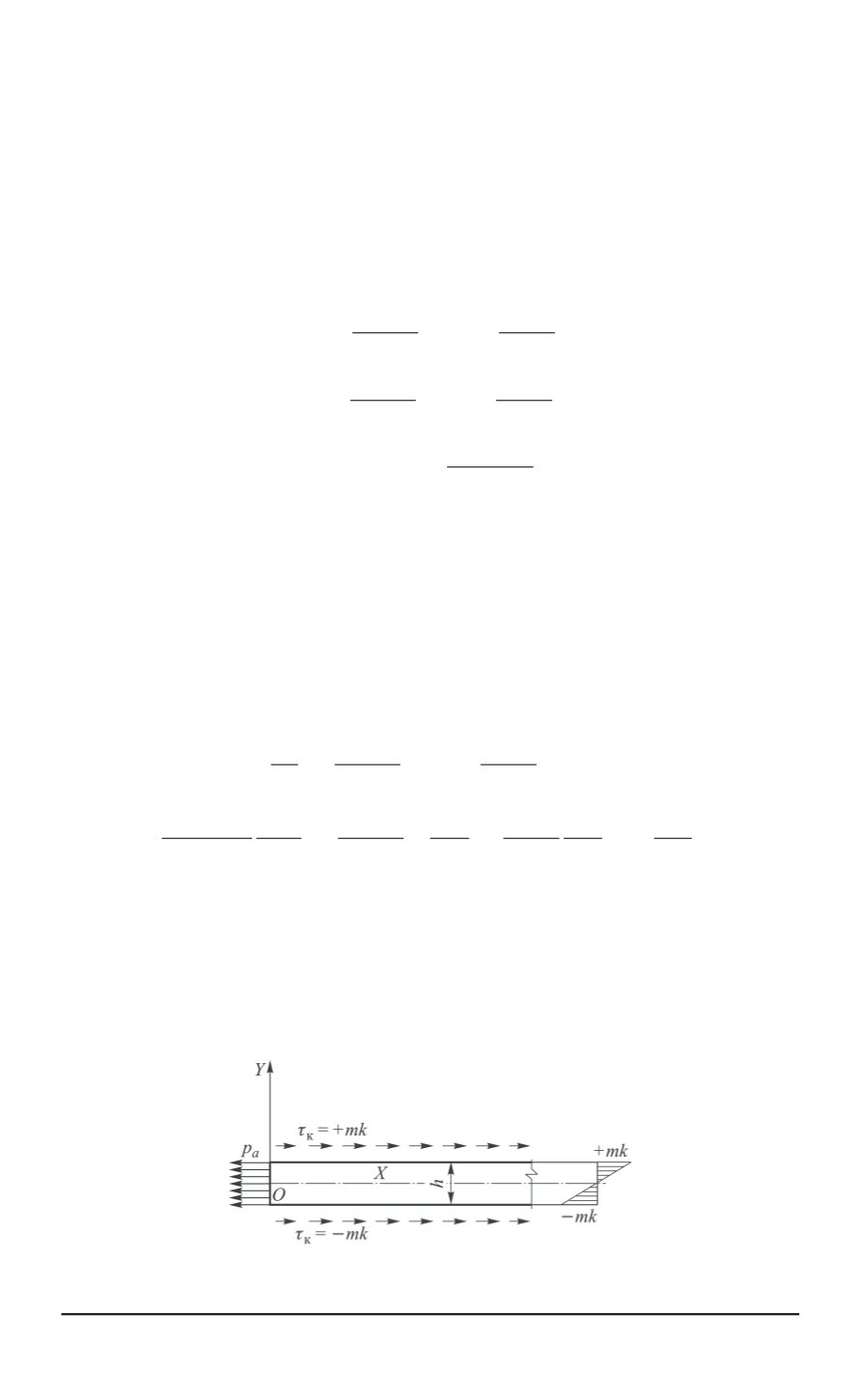
Рассмотрим решение указанных уравнений для полубесконечной
тонкой упругой полосы толщиной
h
, показанной на рис. 2.
Граничные условия задачи для тонкой полосы.
При расположе-
нии системы координат, как на рис. 2, ось абсцисс
OX
совпадает с
осью симметрии тонкой полосы
Y
= 0
. На оси симметрии полосы,
очевидно, что
τ
xy
= 0
и
v
= 0
.
Рис. 2. Тонкая упругая полоса толщиной
h
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 3 105

















