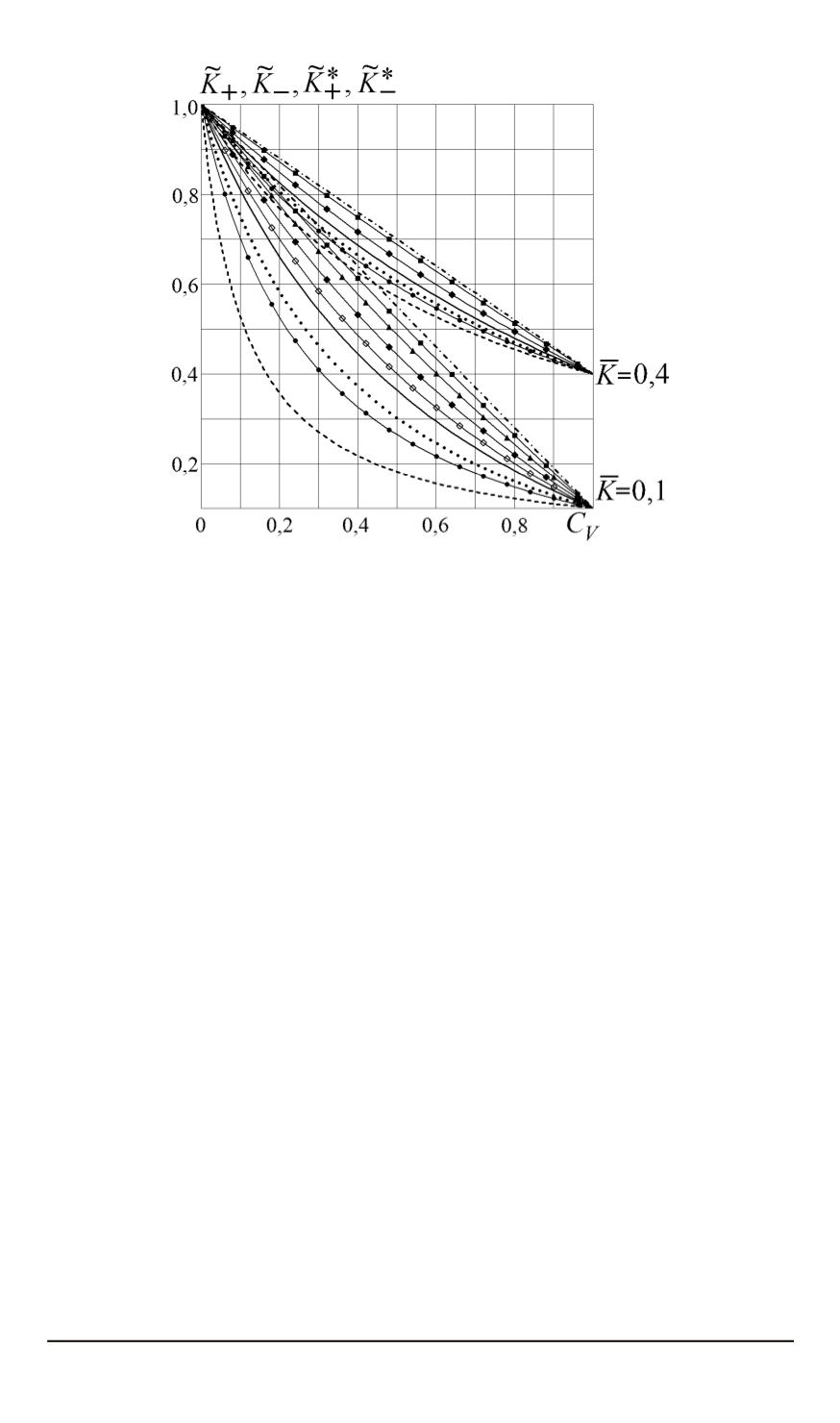
Рис. 2. Зависимости от объемной концентрации
C
V
включений при
ˉ
K
= 0
,
1
и
ˉ
K
= 0
,
4
:
штрихпунктирные и штриховые линии — двусторонние оценки
˜
K
+
=
K
+
/K
◦
и
˜
K
−
=
K
−
/K
◦
; уточненные двусторонние оценки
˜
K
+
и
˜
K
−
при
ˉ
G
◦
= 0
,
4
и
различных значениях
ˉ
G
(сплошные кривые —
ˉ
G
= 1
, штриховые —
ˉ
G
= 0
,
5
, тонкие
сплошные с кружками —
ˉ
G
= 0
,
3
, со светлыми и темными ромбами —
ˉ
G
= 1
,
5
и
ˉ
G
= 2
,
5
, с треугольниками и квадратами —
ˉ
G
= 5
и
ˉ
G
= 10
соответственно)
Следует отметить, что использование вириального разложения [6]
и учет взаимодействия шарового включения с окружающей его матри-
цей [8, 9] приводят для объемного модуля к формулам, совпадающим
с одной из представленных уточненных оценок. При
ˉ
K
= 1
/
0
,
1 = 10
и
ˉ
K
= 1
/
0
,
4 = 2
,
5
вид всех графиков на рис. 2 не изменится, если
все безразмерные величины нормировать не по
K
◦
, а по
K
•
, и по оси
абсцисс вместо
C
V
отсчитывать величину
1
−
C
V
.
При совпадении модулей сдвига матрицы и включений
Δ ˉ
G
1
=
= Δ ˉ
G
2
= 0
, т.е. совпадают уточненные верхняя и нижняя оценки
модуля сдвига композита, что (как и в случае с объемным модулем
композита) формально равносильно равенству
G
=
G
◦
=
G
•
. Одна-
ко при
G
◦
6
=
G
•
эти оценки совпадут лишь при выполнении условия
ˉ
G
1
= ˉ
G
2
, что в общем случае маловероятно. На рис. 3 при
ˉ
G
= 0
,
3
и
ˉ
G
= 0
,
5
представлены графики зависимостей от
C
V
двусторонних оце-
нок
˜
G
+
и
˜
G
−
(штрихпунктирные и штриховые линии соответственно),
построенные по вторым формулам (5) и (6), а также графики зависи-
мостей уточненных двусторонних оценок
˜
G
+
= ˜
G
+
−
min(Δ ˉ
G
1
,
Δ ˉ
G
2
)
и
˜
G
−
= ˜
G
+
−
max(Δ ˉ
K
1
,
Δ ˉ
K
2
)
, построенные при различных значениях
ˉ
G
0
, где
ˉ
G
0
может быть равным как
ˉ
G
1
, так и
ˉ
G
2
(сплошные кривые
соответствуют
ˉ
G
0
= 1
,
1296
, штриховые —
ˉ
G
0
= 0
,
2735
, со светлыми
60 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 5


