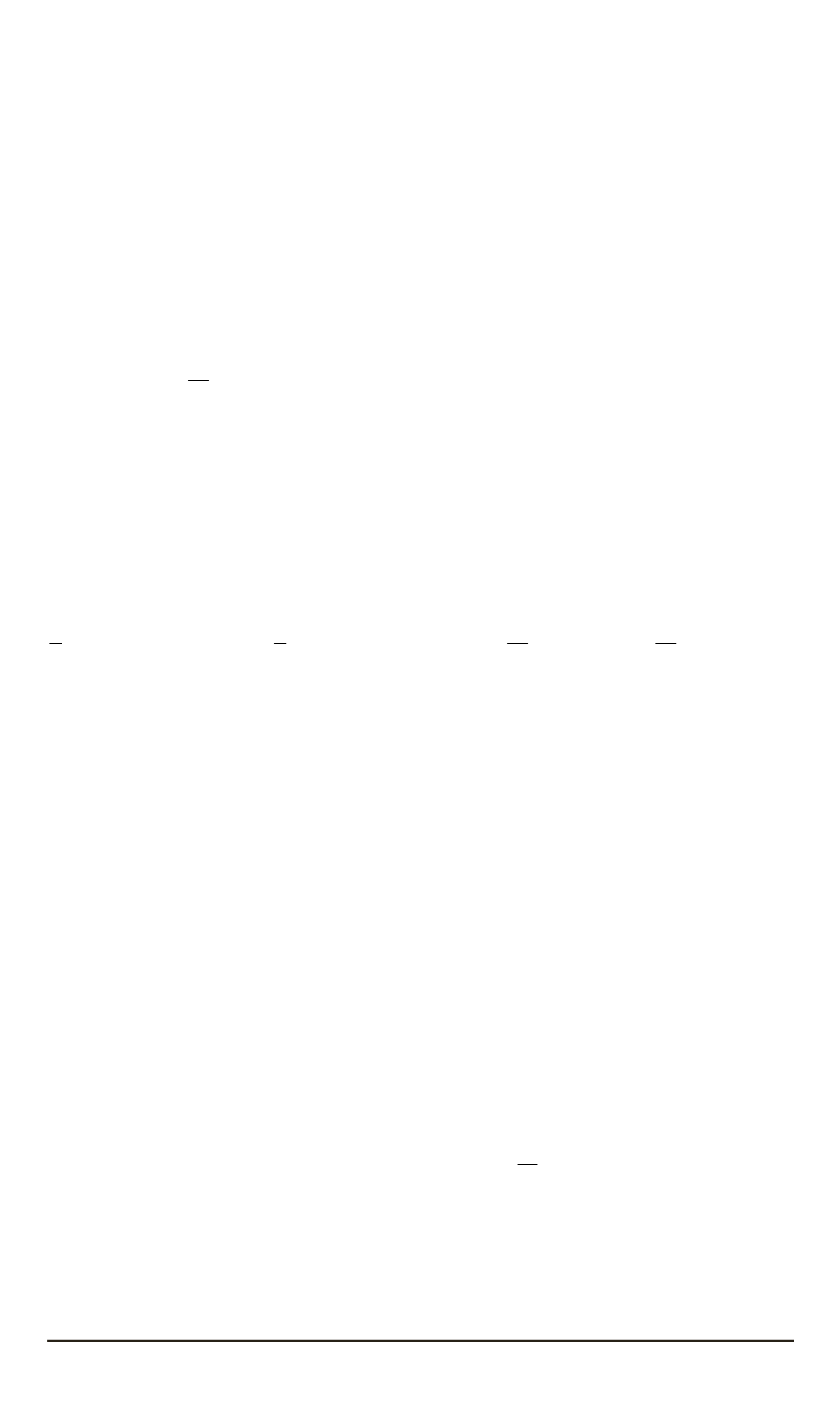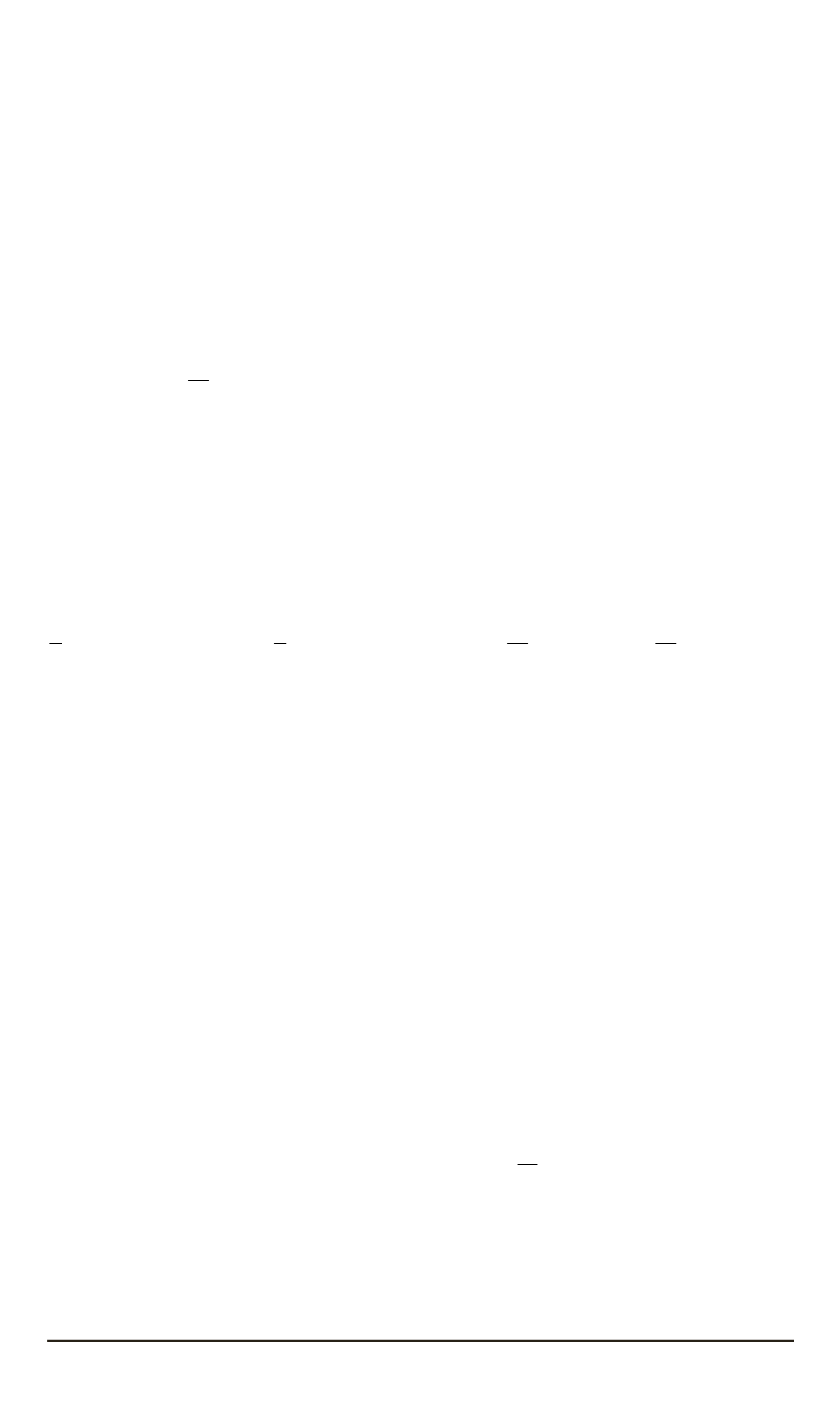
где тензоры
ˆ
σ
и
ˆ
ε
соответствуют истинному напряженно-деформиро-
ванному состоянию среды, удовлетворяющему условиям равновесия
и совместности деформаций. Из сопоставления левой и правой частей
цепочки равенств (8) следует, что принятое допущение основано на
пренебрежении слагаемым
h
ˆ
σ
0
i ∙ ∙h
ˆ
ε
0
i
по сравнению с
h
ˆ
σ
i ∙ ∙h
ˆ
ε
i
. Это
допущение позволяет показать, что оценки (5) и (6) являются двусто-
ронними по отношению к эффективным значениям
K
и
G
модулей
упругости рассматриваемого композита.
При отсутствии объемных сил и задании на поверхности объема
V
кинематических граничных условий функционал Лагранжа, достига-
ющий минимума на истинном распределении перемещений в замкну-
той области
V
=
V
S
S
[16], совпадает со второй частью цепочки
равенств (8). Этот функционал допустимо рассматривать на непре-
рывных и кусочно-дифференцируемых по пространственным коор-
динатам распределениях перемещений, удовлетворяющих кинемати-
ческим граничным условиям. Тогда при допустимом однородном де-
формированном состоянии, определяемом тензором
ˆ
ε
0
=
h
ˆ
ε
i
, с учетом
равенств (4) и (8) можно записать
1
2
Z
V
ˆ
ε
0
∙ ∙
C
∙ ∙
ˆ
ε
0
dV
>
1
2
Z
V
ˆ
ε
∙ ∙
C
∙ ∙
ˆ
ε dV
=
V
2
h
ˆ
σ
i ∙ ∙h
ˆ
ε
i
=
V
2
ˆ
ε
0
∙ ∙
C
∙ ∙
ˆ
ε
0
.
Отсюда последовательно получим неравенства
Z
V
( ˆC
−
ˆC)
dV
>
ˆO
4
,
Z
V
ˆV
∙∙∙∙
( ˆC
−
ˆC)
dV
>
0
,
Z
V
ˆD
∙∙∙∙
( ˆC
−
ˆC)
dV
>
0
.
Из второго и третьего неравенств с учетом первой формулы (1) и ра-
венств (2) следует
K
◦
(1
−
C
V
)+
K
•
C
V
>
K
и
G
◦
(1
−
C
V
)+
G
•
C
V
>
G
, что,
согласно формулам (5), равносильно неравенствам
K
+
>
K
и
G
+
>
G
,
т.е. значения
K
+
и
G
+
действительно являются верхними оценками
соответственно для
K
и
G
.
Аналогичным путем можно показать, что значения
K
−
и
G
−
явля-
ются нижними оценками эффективных значений
K
и
G
. Для этого
достаточно рассмотреть представительный объем
V
композита с сило-
выми граничными условиями на его поверхности. Тогда третья часть
цепочки равенств (8), взятая с обратным знаком, совпадет с функци-
оналом Кастилиано, достигающим максимума на истинном распре-
делении напряжений в замкнутой области
V
[16]. Этот функционал
допустимо рассматривать на статически возможных распределени-
ях напряжений. При допустимом однородном напряженном состоя-
нии, определяемом тензором
ˆ
σ
0
=
h
ˆ
σ
i
, с учетом равенств (4) и (8)
запишем
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2014. № 5 57