−
1
2
Z
V
ˆ
σ
0
∙ ∙
ˆS
∙ ∙
ˆ
σ
0
dV
6
−
1
2
Z
V
ˆ
σ
∙ ∙
ˆS
∙ ∙
ˆ
σ dV
=
=
−
V
2
h
ˆ
σ
i ∙ ∙h
ˆ
ε
i
=
−
V
2
ˆ
σ
0
∙ ∙
ˆS
∙ ∙
ˆ
σ
0
.
Отсюда последовательно получим неравенства
Z
V
( ˆS
−
ˆS)
dV
>
O
4
,
Z
V
ˆV
∙ ∙ ∙ ∙
( ˆS
−
ˆS)
dV
>
0
,
Z
V
ˆD
∙ ∙ ∙ ∙
( ˆS
−
ˆS)
dV
>
0
.
Из второго и третьего неравенств с учетом второй формулы (1)
и равенств (2) следует
(1
−
C
V
)
/K
◦
+
C
V
/K
•
>
1
/K
и
(1
−
C
V
)
/G
◦
+
+
C
V
/G
•
>
1
/G
, что, согласно формулам (6), равносильно неравенствам
K
−
6
K
и
G
−
6
G
, т.е. значения
K
−
и
G
−
, действительно, являются
нижними оценками эффективных значений соответствующих модулей
упругости композита.
Если в качестве первого приближения к эффективным значениям
K
и
G
принять средние арифметические полученных оценок, то каждая
полуразность
Δ ˉ
K
= ( ˜
K
+
−
˜
K
−
)
/
2
и
Δ ˉ
G
= ( ˜
G
+
−
˜
G
−
)
/
2
будет ха-
рактеризовать наибольшую возможную относительную погрешность
такого приближения. Используя формулу (7), находим, что разность
Δ ˉ
G
достигает максимального значения
Δ ˉ
G
max
= (1
−
√
ˉ
G
)
2
/
2
при
объемной концентрации включений
C
(
G
)
V
=
√
ˉ
G/
(1+
√
ˉ
G
)
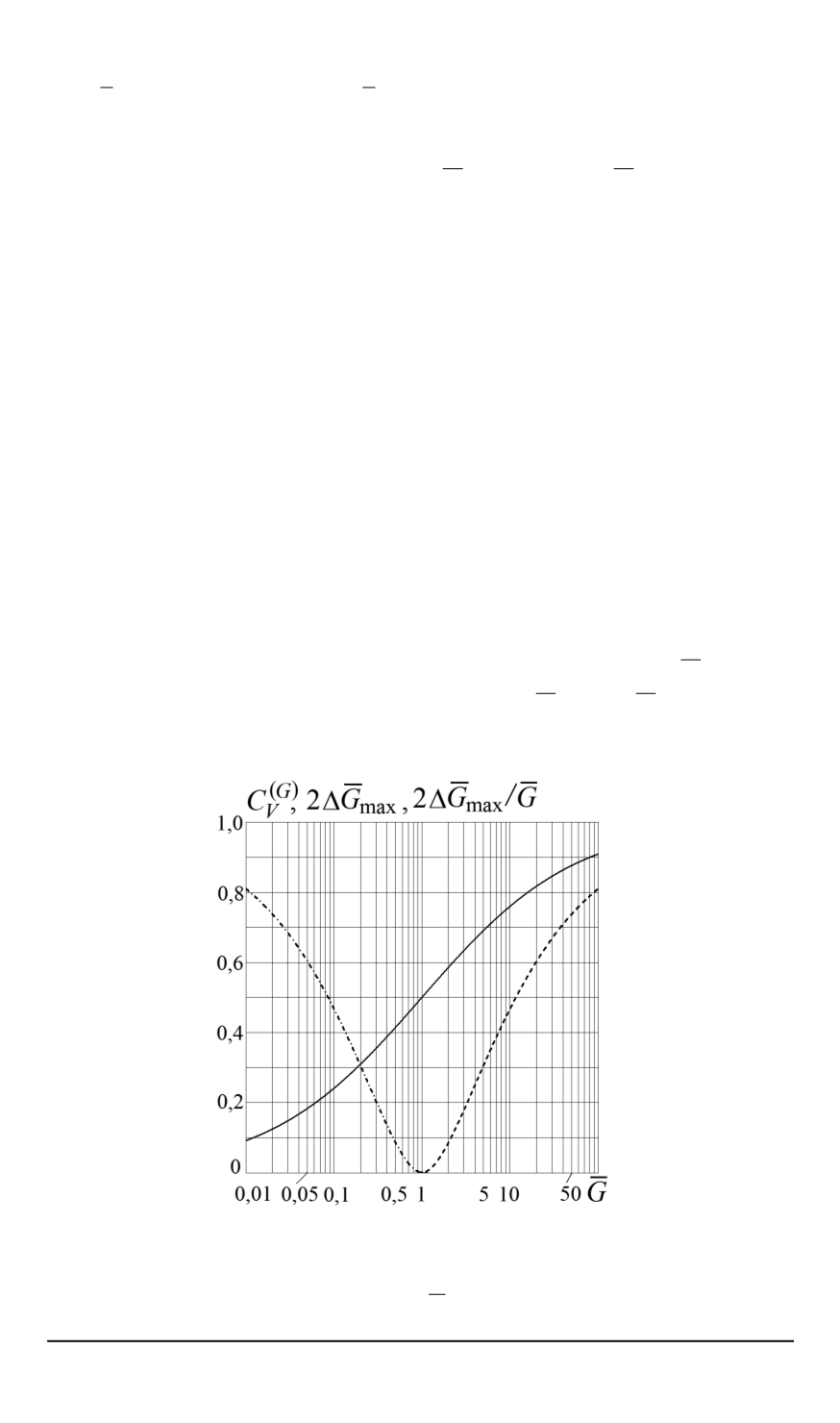
. На рис. 1 в
полулогарифмических координатах приведены графики зависимостей
Рис. 1. Зависимости от параметра
ˉ
G
:
сплошная кривая — объемная концентрация
C
(
G
)
V
включений; штрихпунктирная —
2Δ ˉ
G
max
при
ˉ
G
6
1
; штриховая —
2Δ ˉ
G
max
/G
при
ˉ
G
>
1
58 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2014. № 5


