невозможна потеря устойчивости непрерывного процесса резания
.
Физически понятно, что при достаточно жестком креплении инстру-
мента —
k
ax
→ ∞
, т.е. энергии, поступающей от процесса резания,
недостаточно, чтобы возбудить систему. Внешнее трение увеличива-
ет порог возбуждения автоколебаний. Соответствующие критическому
значению параметра (14) значения частоты
s
и параметра
F
ax
опреде-
ляются из уравнений (12) как
tg (2
πs
) =
− √
1 + 2
ζ
ζ
и
F
ax
=
s
√
1 + 2
ζ
.
Параметрическое представление решения системы (12) имеет вид
K
(
s
;
ζ
) = 2
ζ
[
S
Φ(
s
;
ζ
)]
−
1
;
F
ax
(
s
;
ζ
) =
−
s
Φ(
s
;
ζ
);
C
= cos (2
πs
);
S
= sin (2
πs
);
Φ(
s
;
ζ
) =
S
h
(1
−
C
)
ζ
+
p
(1
−
C
)
2
ζ
2
+
S
2
i
−
1
.
(15)
Из уравнений (15) следует, что имеется возможность выделить уни-
версальные периодические функции
K
(
s
;
ζ
) =
K
(
s
+ 1;
ζ
)
,
F
ax
(
s
;
ζ
)
s
=
F
ax
(
s
+ 1;
ζ
)
(
s
+ 1)
,
которые позволяют представить информацию о границах областей не-
устойчивости в единой форме для всех зон (13), т.е. достаточно рас-
смотреть один интервал
I
s
=
n
1
2
< s <
1
o
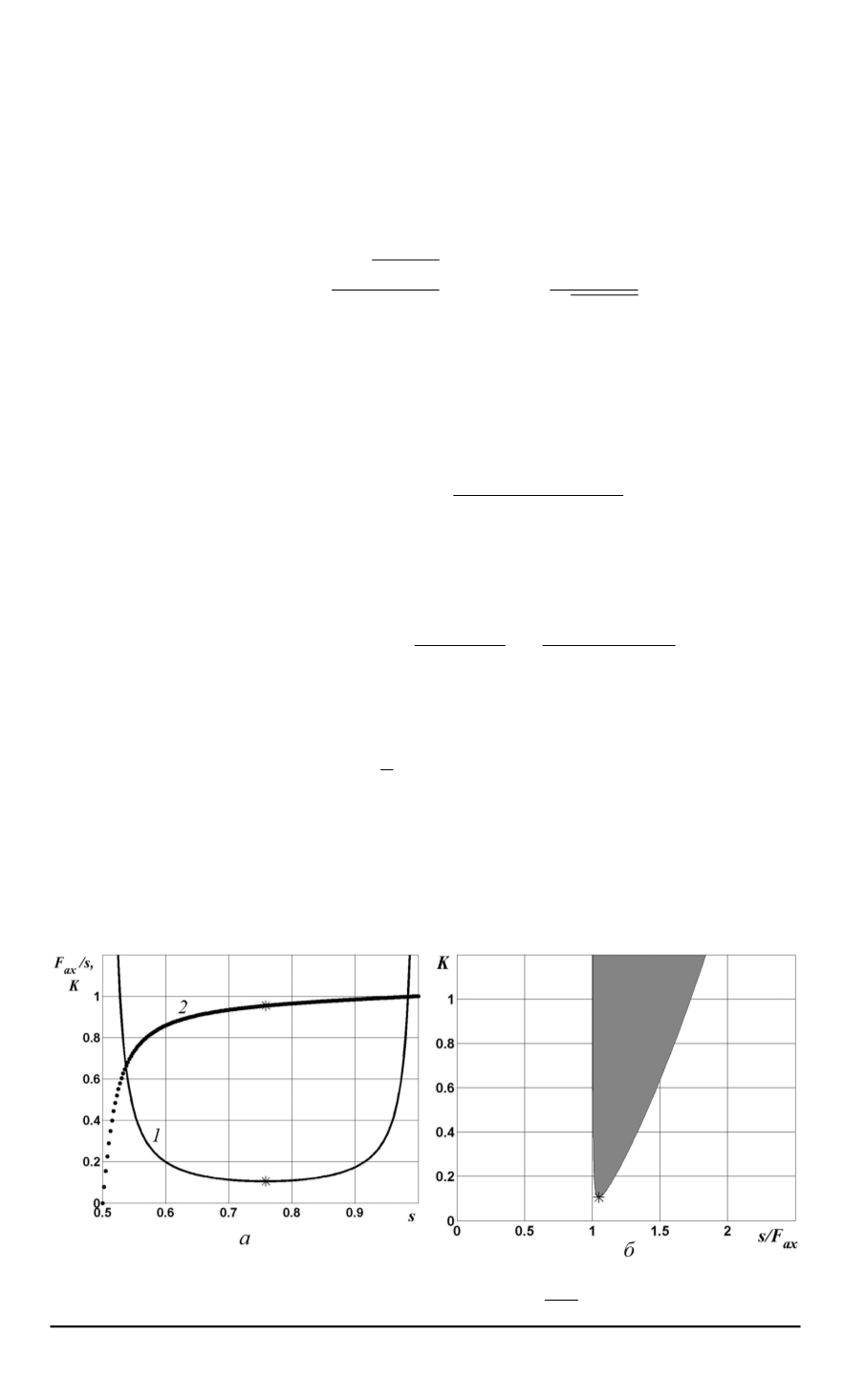
(рис. 4). Из графиков видно,
что при
K > K
(внутри заштрихованной зоны, см. рис. 4,
б
) процесс
непрерывного резания неустойчив. Существует наименьшая скорость
резания (правая полуветвь границы зоны динамической неустойчи-
вости), при превышении которой процесс непрерывного резания ста-
Рис. 4. Границы областей устойчивости:
1
—
K
,
2
—
F
ax
s
.
12 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 1


