Δ
j
(
β
) = [
Z
0
(
y
5
(
β
))
−
Z
0
(
y
5
(0))] +
y
1
(
β
)
−
H
+
y
5
(
β
)
−
Λ
J
β
−
1
n
c
;
η
j
(
β
) = max (0
,
Δ
j
(
β
)) ;
Λ
j
(
β
) = Λ
J
β
−
1
n
c
+
η
j
(
β
);
Λ
j
(
β
) = Λ
0
j
(
β
)
, β
≤
0
, J
= (
j
−
1) +
n
c
f ix
1
j
.
(17)
Таким образом, выбранная модель полностью описывается полу-
ченной системой дифференциально-алгебраических уравнений (16) и
(17) с постоянным запаздыванием. Такие системы удобно интегриро-
вать методом Эйлера–Коши с постоянным шагом и итерациями. При
численном решении систем (16) и (17) принимались следующие не-
изменяемые значения параметров:
n
c
= 2
,
q
= 0
,
75
,
μ
P
= 1
,
μ
ζ
= 1
,
c
ξ
= 0
,
c
ψ
= 0
,
H
= 0
.
Для наглядного представления многообразия различных движений
технологической системы наиболее адекватным методом является ис-
пользование отображения Пуанкаре в виде последовательности экс-
тремумов положения инструмента
(Extr[
ξ
])
или приведенной толщи-
ны снимаемого слоя
(Extr[ˉ
η
])
. При этом на диаграмме для каждо-
го значения параметра показываются все экстремумы отображаемой
функции, попавшие в интервал наблюдения.
Автоколебания системы.
В системах, подобных рассматриваемой
в настоящей работе, при некоторых значениях параметров возможно
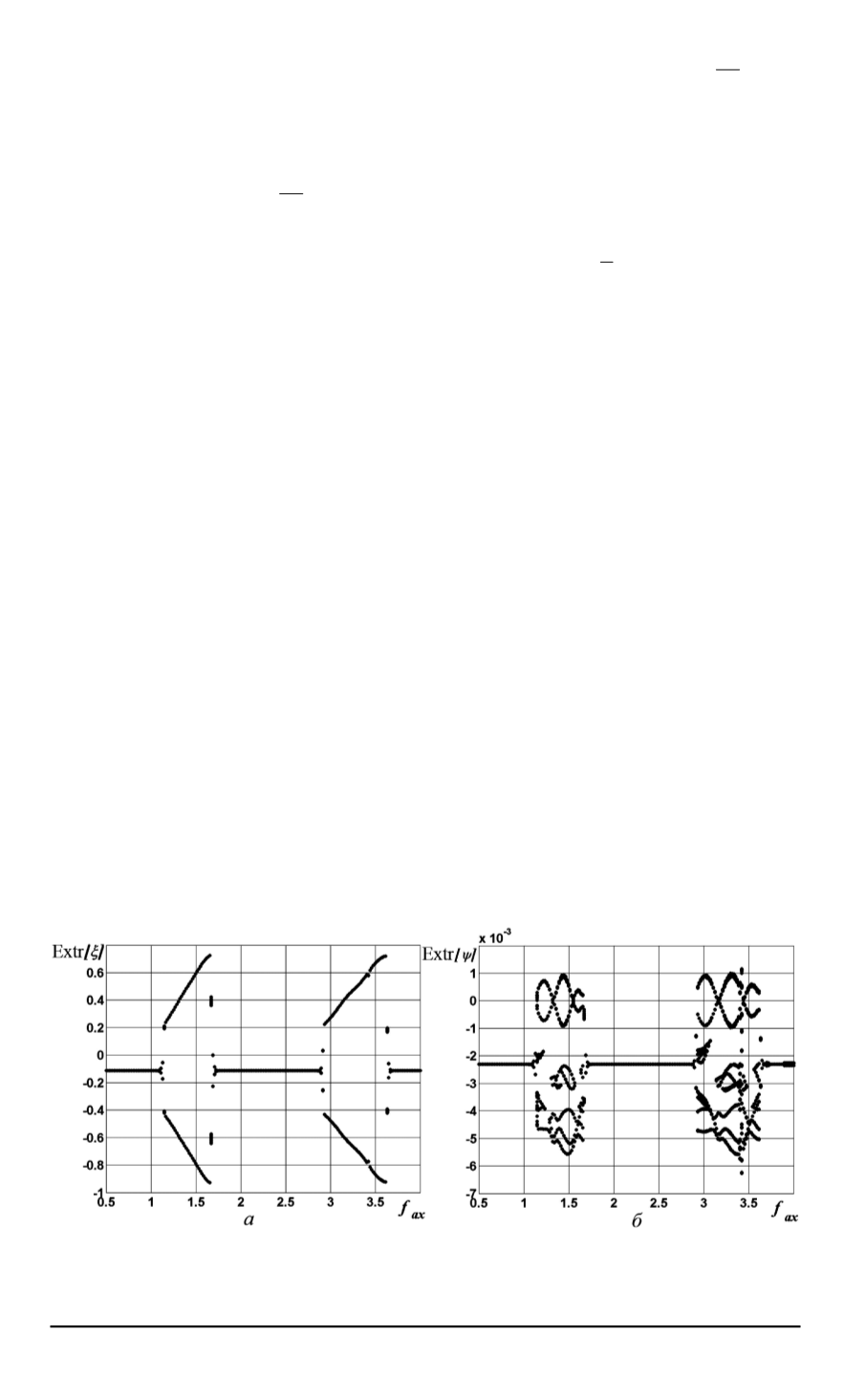
появление автоколебаний. На рис. 5 приведены отображения Пуанкаре
для осевого смещения
ξ
и угла закручивания
ψ
в зависимости от соб-
ственной частоты продольных колебаний инструмента
f
ax
для системы
Рис. 5. Отображения Пуанкаре для осевых колебаний
ξ
(
a
) и крутильных ко-
лебаний
ψ
(
б
) при различных значениях
f
ax
для системы с двумя степенями
свободы
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 1 15


