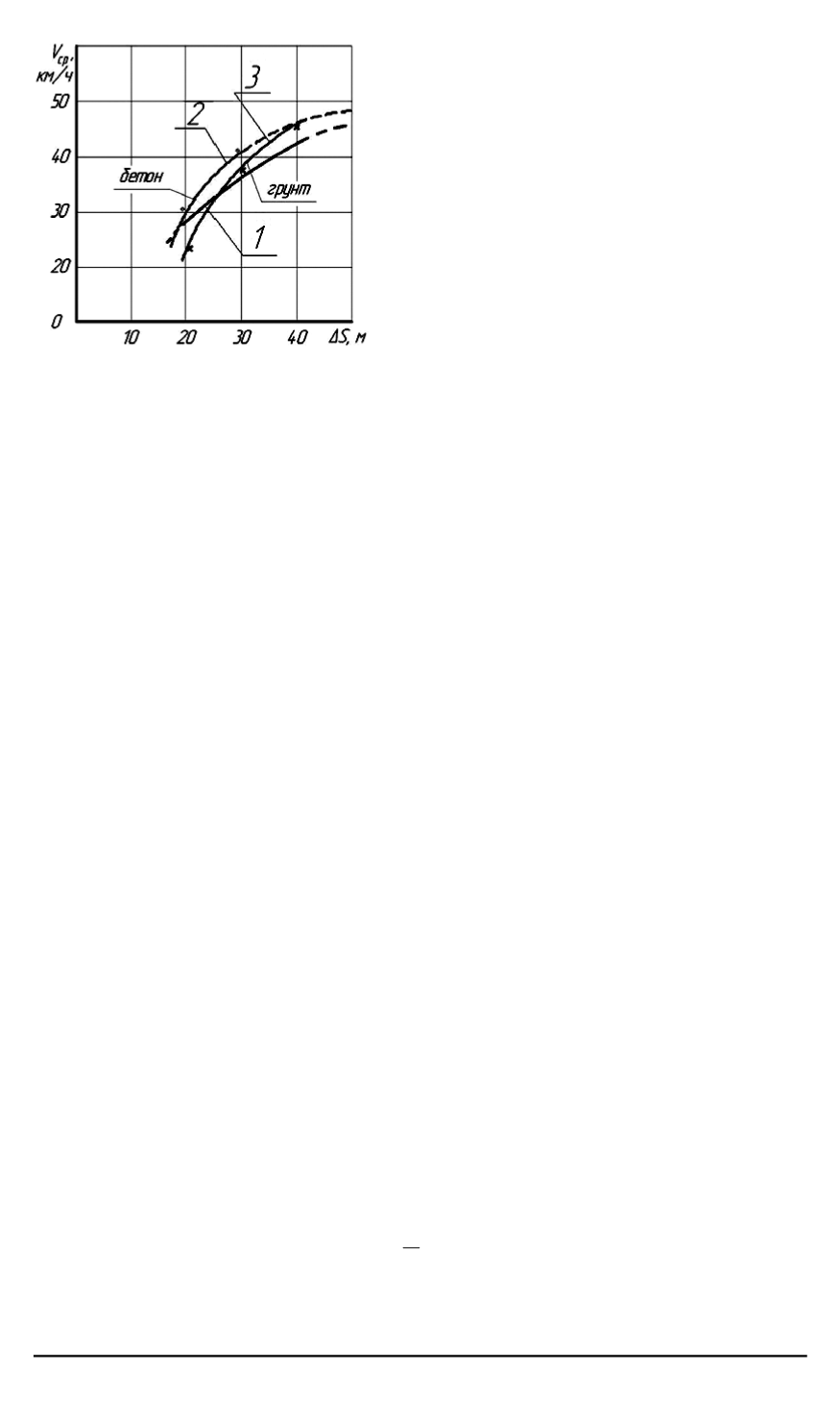
Рис. 4. Зависимость скорости дви-
жения от длины волны тестовой
змейки
по тестовой трассе. При движении
по дорогам со случайным изменени-
ем направления движения совпадение
кривых
1
,
2
и
3
может быть более точ-
ным.
Для прогнозирования подвижно-
сти в качестве аргумента целесо-
образно принять частоту процесса
ω
.
При движении по тестовой змейке
ω
=
πV/
Δ
S
. Если рассматривать
дорожную кривизну как случайную
функцию, то предельную скорость
движения также можно определить по
коэффициенту фазовой напряженно-
сти. Частотная характеристика траек-
тории определяется частной производной курсового угла
ϕ
по пути
S
(
k
=
∂ϕ/∂S
)
. В статистической динамике транспортных машин
[1] показано, что курсовой угол
ϕ
, его производная
∂ϕ/∂S
, а сле-
довательно, и кривизна являются стационарными случайными функ-
циями, обладающими свойствами эргодичности. Если управляющее
воздействие водителя соответствует производной курсового угла на-
правления траектории движения
α
шт
≈
dϕ
(
S
)
, то его можно пред-
ставить стохастической функцией. В силу стационарности случайной
функции
k
(
S
)
ее центрируют относительно математического ожи-
дания
m
к
= 0
. Реакцией гусеничной машины как линеаризованной
системы является случайная функция, спектральная плотность кото-
рой
S
(
ω
) =
|
W
(
ω
)
|
2
Ф
(
ω
)
. Фазово-частотная характеристика и в этом
случае является детерминированной функцией. Предельную скорость
движения также можно определить по зависимости коэффициента фа-
зовой напряженности от частоты. Частота процесса является функцией
числа включений механизма поворота (как число положительных вы-
бросов случайной стационарной функции кривизны траектории нуле-
вого уровня)
ω
= 2
πN V
, где
N
— среднее число включений меха-
низма поворота на единицу пути. Как следует из экспериментальных
данных, предельная частота включений механизма поворота даже вы-
сококвалифицированным водителем не превышает
[
f
]
6
0
,
8
. . .
1
,
0
Гц,
т.е.
[
ω
]
<
5
. . .
6
рад/с.
Корреляционная функция кривизны траектории
k
аппроксими-
руется экспоненциально-косинусоидальной зависимостью
R
k
(
τ
) =
=
σ
2
k
exp(
−
α
|
τ
|
) cos
βτ
или дважды дифференцируемой функцией
R
k
(
τ
) =
σ
2
k
exp(
−
α
|
τ
|
) cos
βτ
+
α
β
sin
β
|
τ
|
.
Последнее выражение позволяет для исследования динамики си-
стемы привлечь аппарат марковских процессов. В соответствии с пря-
80 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 2


