
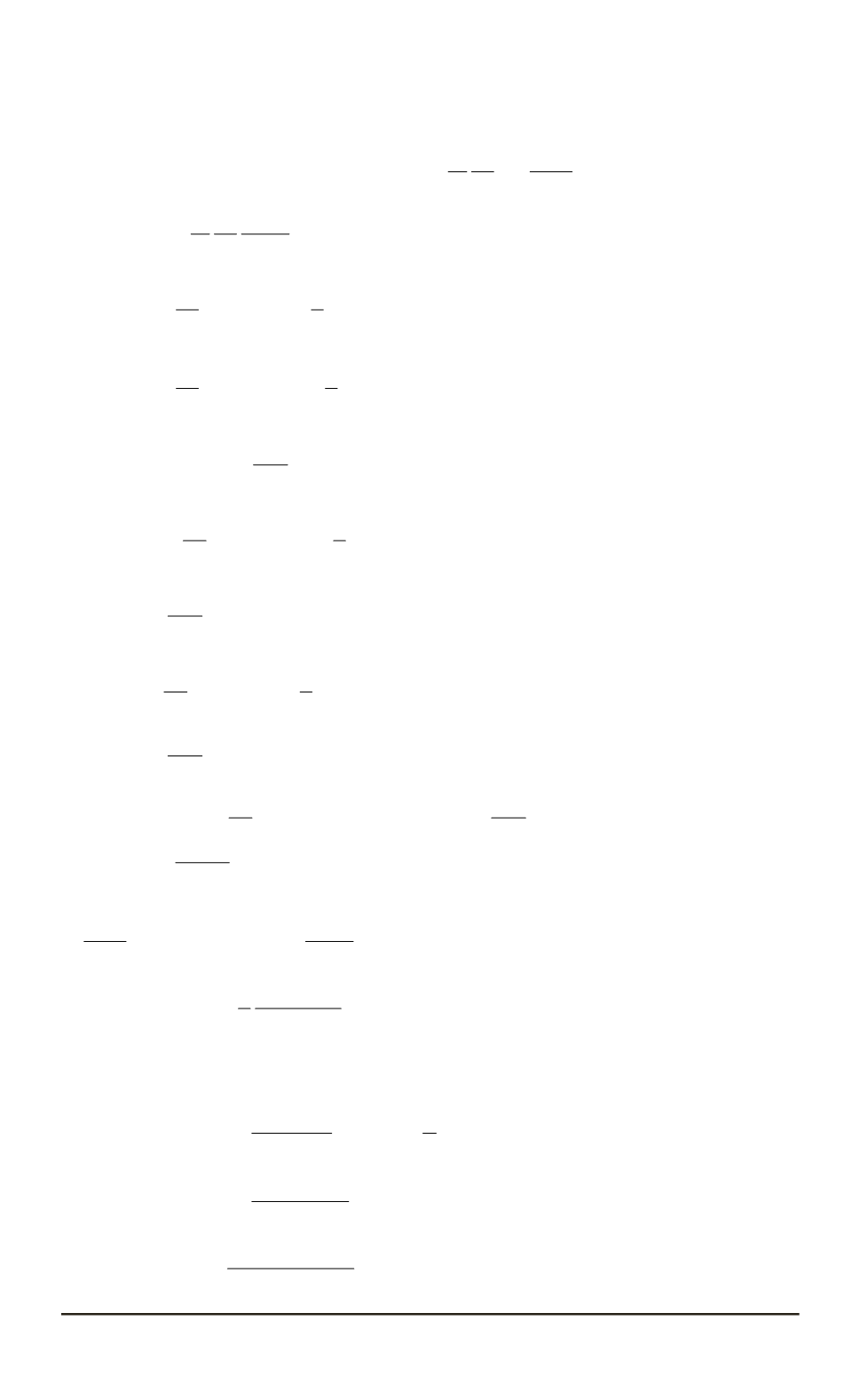
N
1
,k
=
Re
( ˜
f
1
,k
+ ˜
f
2
,k
)
.
2;
N
2
,k
=
Re
(2 ˜
N
k
−
˜
f
1
,k
−
˜
f
2
,k
)
.
2;
S
k
=
Re
( ˜
f
1
,k
−
˜
f
2
,k
)
.
2;
Q
1
,k
=
1
R
D
k
∗
Im
d
˜
N
k
dϑ
;
Q
2
,k
=
−
1
R
D
k
∗
k
sin
ϑ
Im
˜
N
k
;
M
1
,k
=
D
k
∗
Im
˜
N
k
−
1
2
(1
−
μ
)( ˜
f
1
,k
+ ˜
f
2
,k
) ;
M
2
,k
=
D
k
∗
Im
μ
˜
N
k
+
1
2
(1
−
μ
)( ˜
f
1
,k
+ ˜
f
2
,k
) ;
H
k
=
−
(1
−
μ
)
D
2
k
∗
Im
( ˜
f
1
,k
−
˜
f
2
,k
);
ε
1
,k
=
−
D
k
2
∗
Re
μ
˜
N
k
−
1
2
(1 +
μ
)( ˜
f
1
,k
+ ˜
f
2
,k
) ;
χ
1
,k
=
1
2
k
∗
Im
(2 ˜
N
k
−
˜
f
1
,k
−
˜
f
2
,k
);
ε
2
,k
=
D
k
2
∗
Re
˜
N
k
−
1
2
(1 +
μ
)( ˜
f
1
,k
+ ˜
f
2
,k
) ;
χ
2
,k
=
1
2
k
∗
Im
( ˜
f
1
,k
+ ˜
f
2
,k
);
ω
k
= (1 +
μ
)
D
k
2
∗
Re
( ˜
f
1
,k
−
˜
f
2
,k
);
τ
k
=
−
1
2
k
∗
Im
( ˜
f
1
,k
−
˜
f
2
,k
)
,
(16)
где
k
∗
=
√
DEh
;
d
˜
N
k
dϑ
= ˜
C
1
,k
tg
k
ϑ
/2
k
sin
ϑ
F
[˜
a,
1
−
˜
a
; 1 +
k
; sin
2
ϑ
/2]+
+
1
2
˜
a
(1
−
˜
a
)
1 +
k
sin
ϑF
[1 + ˜
a,
2
−
˜
a
; 2 +
k
; sin
2
ϑ
/2]
.
(17)
Значения перемещений определяются [4] формулами:
U
1
,k
=
R
sin
2
ϑ
k
2
−
1
α
1
,k
−
1
k
Rα
2
,k
sin
ϑ
;
U
2
,k
=
R
sin
2
ϑ
k
(
k
2
−
1)
×
×
[
k
2
−
cos
2
ϑ
]
sin
ϑ
ε
2
,k
−
Rχ
2
,k
sin
ϑ
−
α
1
,k
cos
ϑ
;
126 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 3

















