
Алгоритм решения краевой задачи следующий:
1) вычисляют значения разрешающих функций (15) и их произ-
водных (17) в виде (19) (производные
˜
f
1
,k
и
˜
f
2
,k
могут быть получены
непосредственно из уравнений (14));
2) аналогично (20) вычисляют значения искомых величин задачи
(16), (18) до постоянных интегрирования;
3) в остальном действуют аналогично п. 2–7 алгоритма решения
краевой задачи с использованием асимптотической модели.
Вычислительный эксперимент.
Построение расчетной схемы за-
дачи предполагает математическую идеализацию моделируемого объ-
екта. Так, поверхностная нагрузка, распределенная по малой площад-
ке, часто заменяется воздействием сосредоточенной силы. Это объяс-
няется простотой построения алгоритма: не нужно решать дифферен-
циальные уравнения с правой частью, которая появляется при поверх-
ностной нагрузке. При этом в точке приложения силы имеется особен-
ность: ряды искомых параметров задачи не сходятся. Распределение
сосредоточенной силы по линии позволяет обеспечить сходимость ря-
дов искомых величин.
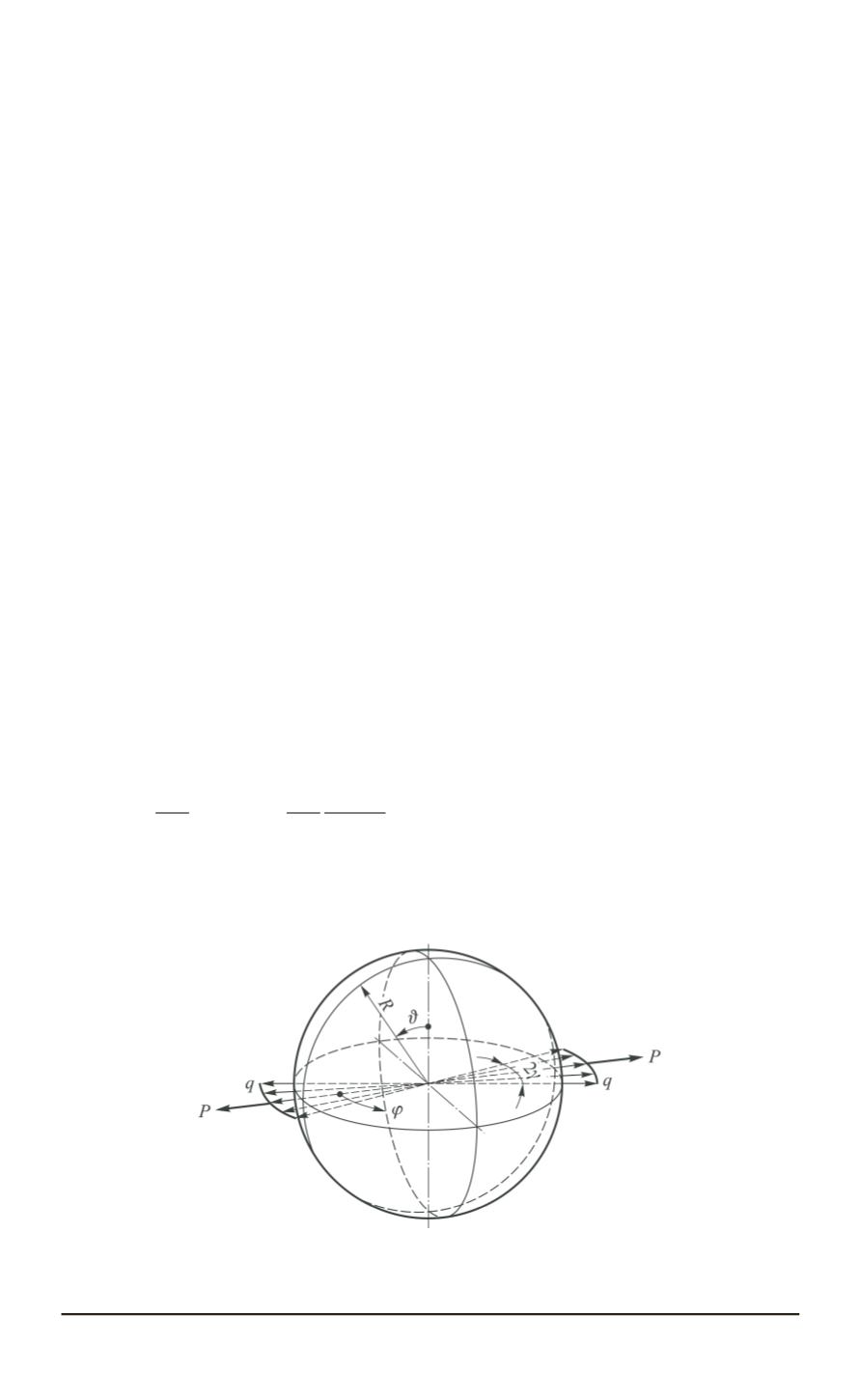
Рассмотрим задачу деформирования сферической оболочки, моде-
ли сферического бака, с параметром
R
/
h
под действием самоуравно-
вешенной силы
P
, распределенной по дуге окружности (рис. 1).
Разложение силы
P
в ряд Фурье имеет вид
q
(
ϕ
) =
∞
X
k
=0
,
2
,
4
,...
q
k
cos
kϕ,
где
q
0
=
P
πR
и
q
k
= 2
P
πR
sin
kγ
kγ
.
В данном случае край оболочки отсутствует. Однако оболочка мо-
жет быть мысленно разделена на два участка параллелью
ϑ
= 90
◦
,
соответствующей линии приложения внешней нагрузки.
Рис. 1. Модель сферического бака (самоуравновешенная сила
P
распределена
по дуге окружности)
128 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 3

















