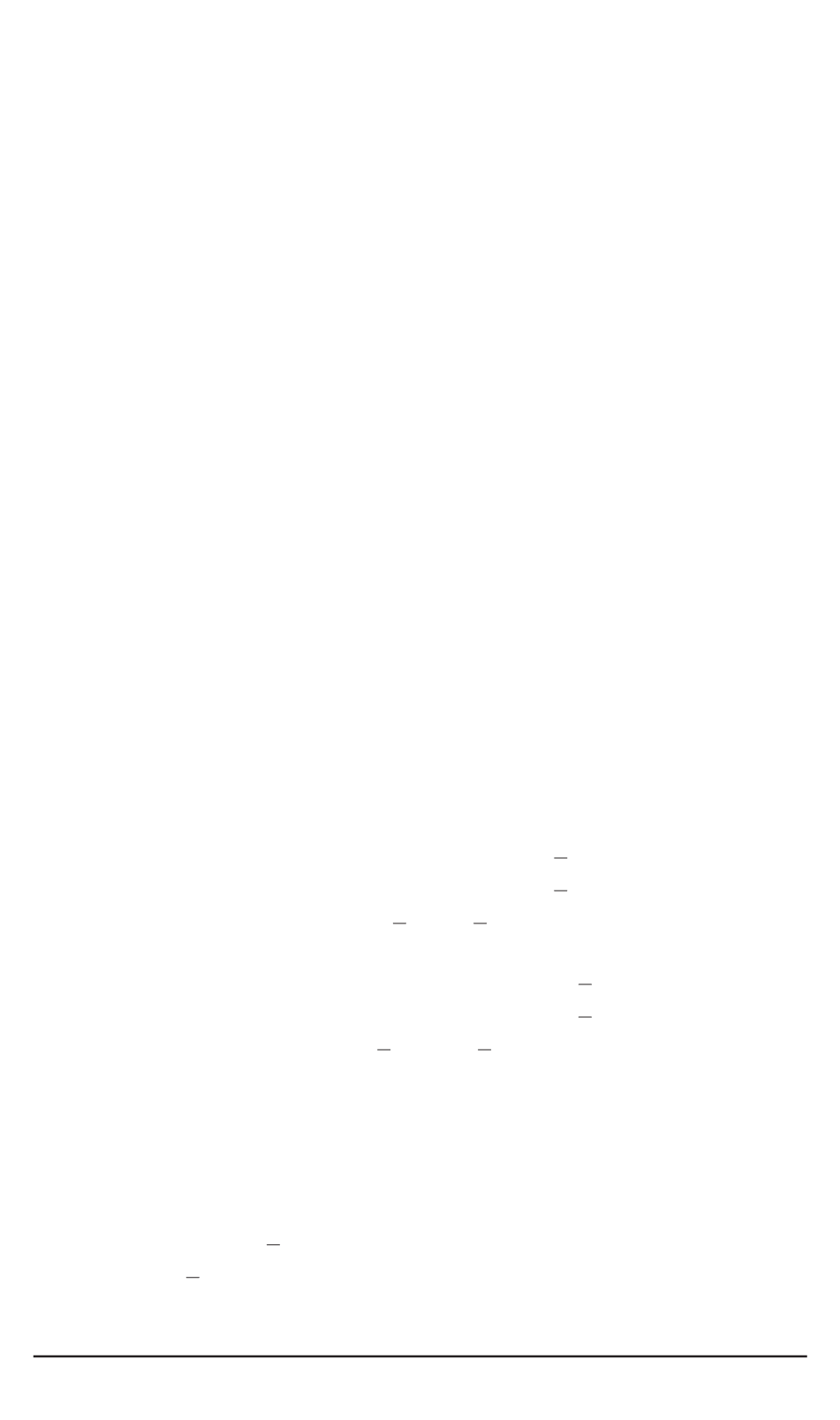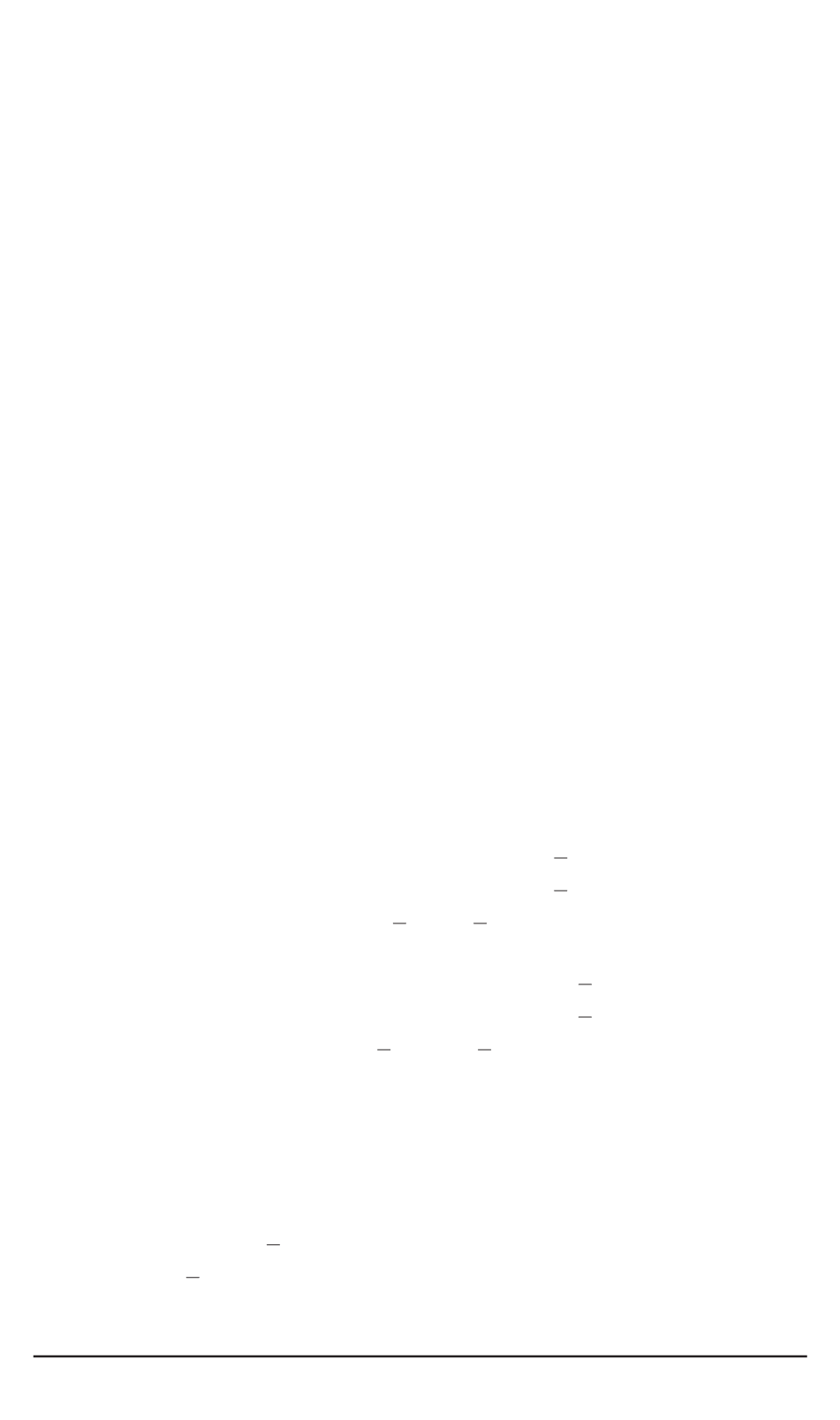
Матрица частных производных
(
А
) = (
∂J
α
/∂σ
ij
)
для системы ин-
вариантов (14) следующая:
(
A
) =
⎛
⎜⎜⎜⎜⎜⎜⎝
1
1
1
2
σ
11
2
σ
22
2
σ
33
3(
σ
2
11
+
σ
2
12
+
σ
2
13
) 3(
σ
2
22
+
σ
2
12
+
σ
2
23
) 3(
σ
2
33
+
σ
2
13
+
σ
2
23
)
0
0
1
0
0
2
σ
33
σ
13
σ
23
−
σ
13
σ
23
0
⇒
⇒
0
0
0
4
σ
23
4
σ
13
4
σ
12
6(
σ
22
σ
23
+
σ
33
σ
23
+
σ
12
σ
13
) 6(
σ
11
σ
13
+
σ
33
σ
13
+
σ
12
σ
23
) 6(
σ
11
σ
12
+
σ
22
σ
12
+
σ
13
σ
23
)
0
0
0
2
σ
23
2
σ
13
0
−
σ
22
σ
13
+
σ
11
σ
13
+2
σ
12
σ
23
−
2
σ
12
σ
13
−
σ
22
σ
23
+
σ
11
σ
23
−
σ
2
13
+
σ
2
23
⎞
⎟⎟⎟⎟⎟⎟⎟⎠
.
Определитель этой матрицы
det(
A
)
≡
0
.
Получаем, что ранг матрицы меньше числа инвариантов в системе
(14) и, следовательно, инварианты, входящие в систему (14), функ-
ционально зависимы. Однако в функциональном базисе (12) и, сле-
довательно, базисе (14) ни один инвариант не является лишним. Для
доказательства используем метод, предложенный в работе [12].
Чтобы доказать, что инвариант
J
1
не может быть выражен через
J
2
,
J
3
,
J
4
,
J
5
,
J
6
, найдем значения инвариантов (12) при
σ
(1)
ij
=
⎛
⎝
0
−
2 1
/
√
6
−
2 0 1
/
√
6
1
/
√
6 1
/
√
6 1
⎞
⎠
и
σ
(2)
ij
=
⎛
⎝
0
2
−
1
/
√
6
2
0
−
1
/
√
6
−
1
/
√
6
−
1
/
√
6
−
1
⎞
⎠
.
Получаем
J
2
(
σ
(1)
ij
) =
J
2
(
σ
(2)
ij
)
,
J
3
(
σ
(1)
ij
) =
J
3
(
σ
(2)
ij
)
,
J
4
(
σ
(1)
ij
) =
J
4
(
σ
(2)
ij
)
,
J
5
(
σ
(1)
ij
) =
J
5
(
σ
(2)
ij
)
,
J
6
(
σ
(1)
ij
) =
J
6
(
σ
(2)
ij
)
, однако
J
1
(
σ
(1)
ij
) =
J
1
(
σ
(2)
ij
)
.
Для доказательства, что в системе инвариантов (12) не являет-
ся лишним инвариант
J
2
, достаточно вычислить инварианты при
σ
(1)
ij
=
⎛
⎝
0 1
/
√
2 0
1
/
√
2 0 0
0
0 0
⎞
⎠
и
σ
(2)
ij
=
⎛
⎝
0 0 1
0 0 0
1 0 0
⎞
⎠
.
92 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2009. № 1