При практической реализации метода для регуляризации задачи к
функции Лагранжа
(5)
добавляют слагаемое
(1
/
2
k
)
{
λ
}
т
{
λ
}
[8].
В ре
-
зультате второе уравнение системы
(6),
описывающее условия точеч
-
ного контакта
,
заменяется следующим
:
[
C
]
т
{
∆
}
+ (1
/k
)
{
λ
}
=
{
η
}
.
Применительно к задаче обжатия шины
,
решаемой по оболочечной мо
-
дели
,
смысл добавленного слагаемого
(1
/k
)
{
λ
}
очевиден
—
это дефор
-
мации протектора
.
В случае больших перемещений упругого тела
,
какие имеют место
при обжатии шины
,
алгоритм решения контактной задачи дополняется
внутренним
(
по отношению к поиску области контакта
)
итерационным
процессом
,
направленным на выполнение нелинейных уравнений рав
-
новесия
.
При использовании метода Ньютона уравнения итерационно
-
го процесса имеют вид
:
[
K
t
]
j
d
{
∆
}
j
+1
+ [
C
]
{
λ
}
j
+1
=
{
f
} − {
g
}
j
;
[
C
]
т
d
{
∆
}
j
+1
+ (1
/k
)
{
λ
}
j
+1
=
{
η
} −
[
C
]
т
{
∆
}
j
;
{
∆
}
j
+1
=
{
∆
}
j
+
d
{
∆
}
j
+1
, j
= 0
,
1
,
2
,
· · ·
,
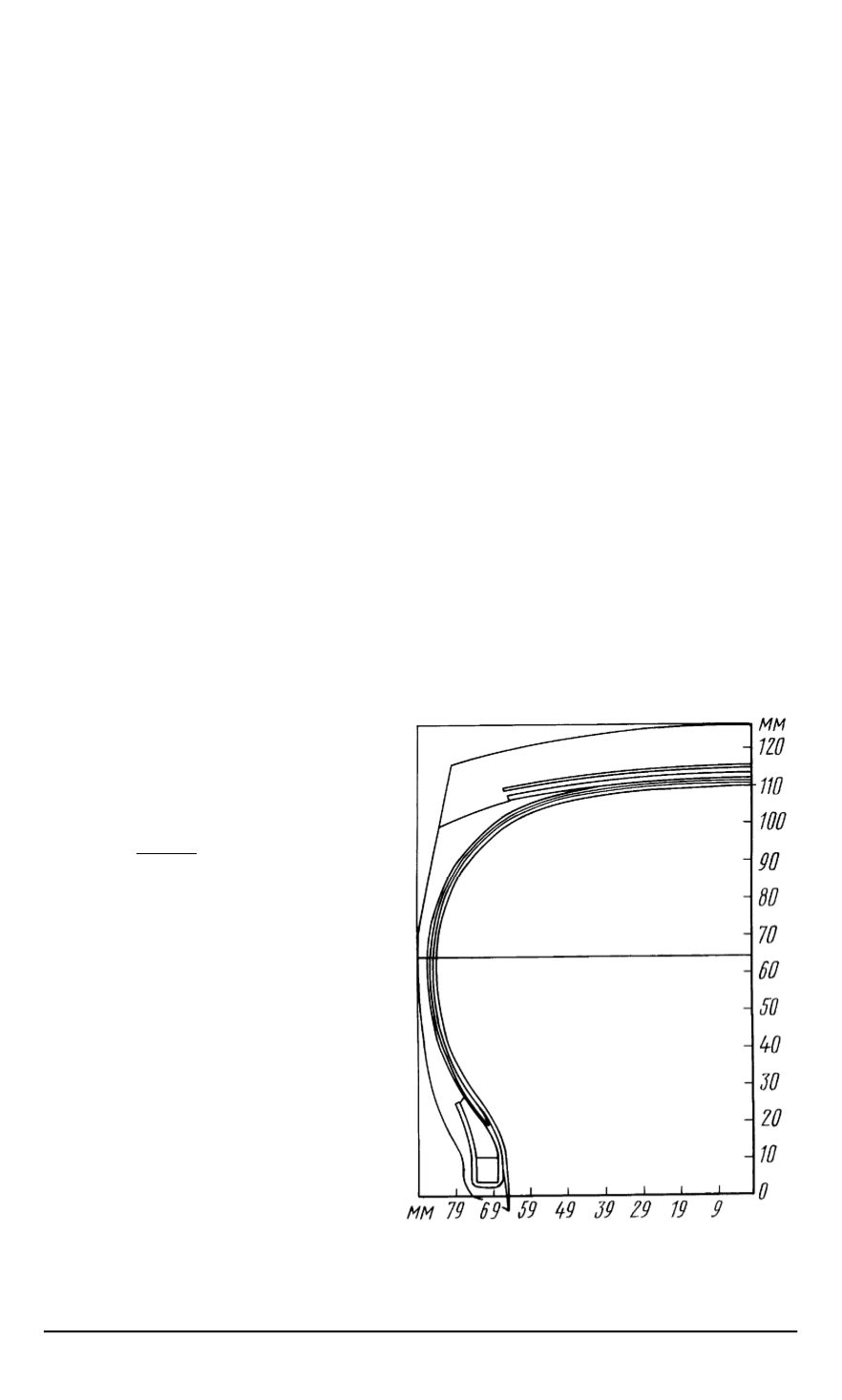
Рис
. 1.
Профиль легковой радиальной ши
-
ны
175/70R13
где
{
∆
}
j
,
d
{
∆
}
j
+1
—
при
-
ближенные значения переме
-
щений и малые поправки к
ним
;
{
g
}
j
—
вектор внутренних
сил при перемещениях
{
∆
}
j
;
[
K
t
]
j
=
∂
{
g
}
∂
{
∆
}
—
матрица тан
-
генциальной жесткости при пе
-
ремещениях
{
∆
}
j
.
Оболочечная модель ши
-
ны
.
Для расчета автомобиль
-
ной шины
(
рис
. 1)
восполь
-
зуемся простейшим вариан
-
том нелинейной теории сло
-
истых оболочек
,
в которой
деформации поперечного сдви
-
га учитываются по модели
Тимошенко
.
Эта теория и ее
уточненные варианты приме
-
нялись для анализа напряжен
-
ного состояния шин в работах
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Машиностроение
”. 2004.
№
3 17


