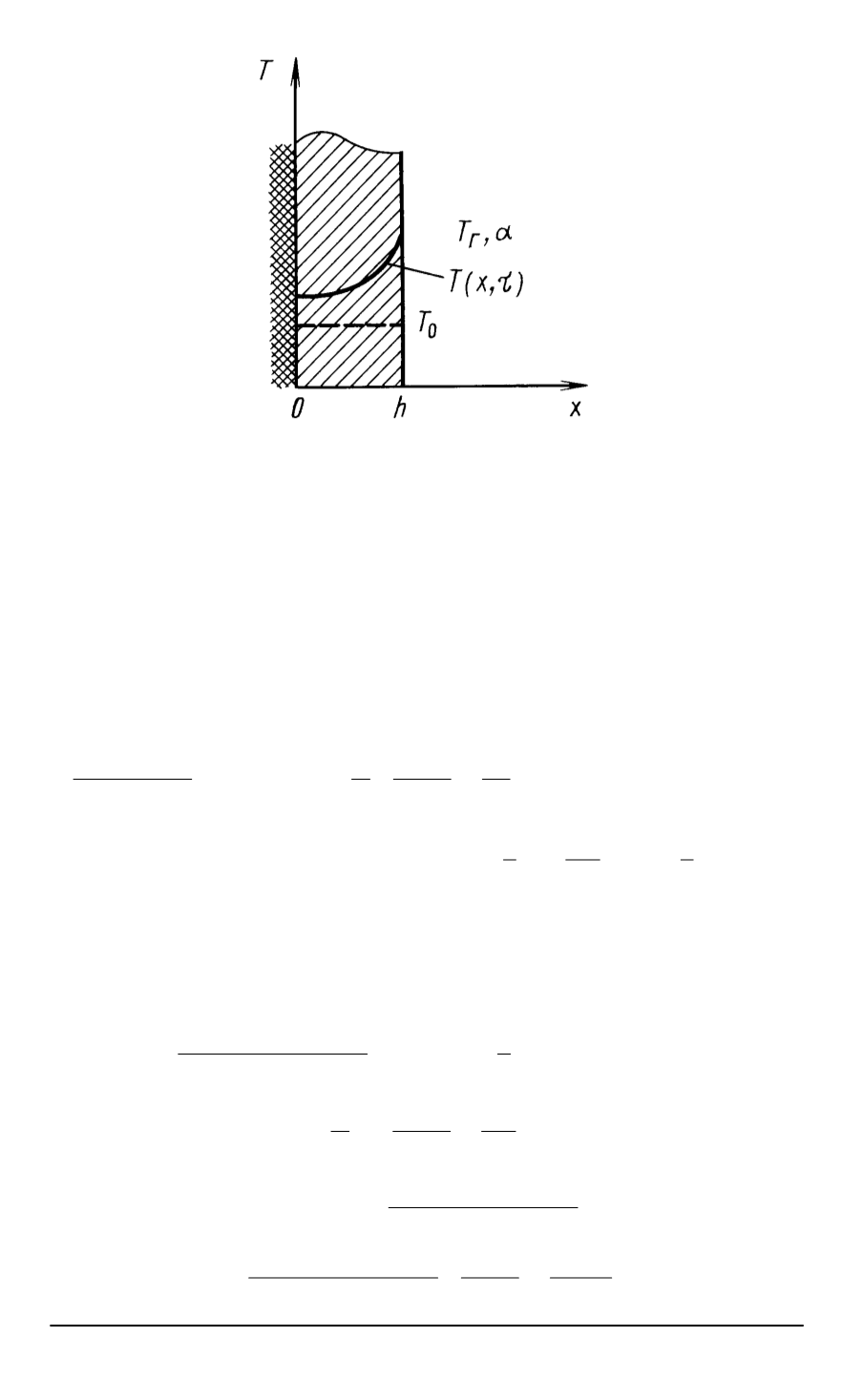
Рис
. 2.
Распределение температуры в изолированной пластине
,
нагреваемой го
-
рячим газом
,
q
v
=
0
С помощью выражения
(38)
можно найти решение задачи для пла
-
стины
,
не имеющей внутренних источников теплоты и нагреваемой с
двух сторон
.
Примем
Po
=
0.
Если пластина размещена в среде с постоянной температурой
(
T
c1
=
T
c2
=
T
c
и
Bi
1
=
Bi
2
=
Bi),
формула
(38)
принимает вид
T
(
x
,
τ
)
−
T
c
T
0
−
T
c
=
∞
∑
n
=
1
e
(
−
µ
2
n
Fo
)
1
N
µ
sin
µ
n
µ
n
+
Bi
µ
2
n
(
1
−
cos
µ
n
)
¶
×
×
Ã
cos
µ
µ
n
x
h
¶
+
Bi
1
µ
n
sin
µ
µ
n
x
h
¶ !
,
(39)
e
сли температуры с разных сторон пластины различны и равны соот
-
ветственно
T
c1
и
T
c2
,
то решение имеет другой вид
:
T
=
T
c1
+
(
T
c2
−
T
c1
)
Bi
1
+
Bi
1
Bi
2
+
Bi
2
Bi
2
µ
1
+
Bi
1
x
h
¶
+
+
∞
∑
n
=
1
e
(
−
µ
2
n
Fo
)
1
N
( µ
sin
µ
n
µ
n
+
Bi
1
µ
2
n
(
1
−
cos
µ
n
)
¶
×
×
µ
T
0
−
T
c1
−
(
T
c2
−
T
c1
)
Bi
2
Bi
1
+
Bi
1
Bi
2
+
Bi
2
¶
−
−
(
T
c2
−
T
c1
)
Bi
1
Bi
2
Bi
1
+
Bi
1
Bi
2
+
Bi
2
µ
sin
µ
n
µ
n
+
cos
µ
n
µ
2
n
−
10 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2003.
№
4


