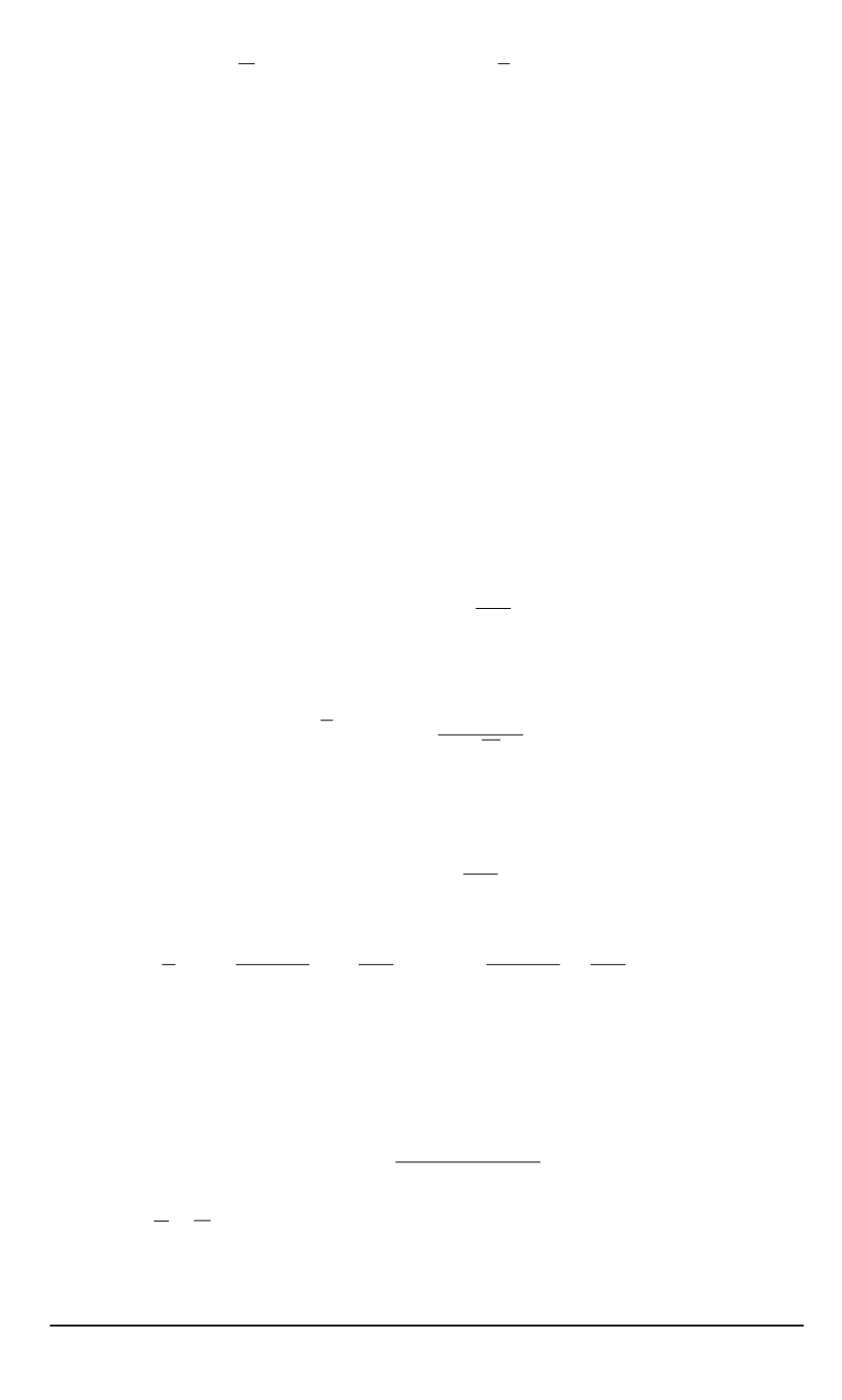
θ
∗
(
0
) =
1
Z
0
ρ
(
ξ
)
θ
∗
(
ξ
,
0
)
k
(
µ
n
,
ξ
)
d
ξ
(22)
(
ρ
(
ξ
)
—
весовая функция
,
µ
n
—
собственные числа
).
В рассматриваемом случае
(
плоская пластина
)
весовая функция
ρ
(
ξ
) =
1 [7],
а ненормированное ядро интегрального преобразования
k
(
µ
n
,
ξ
)
находят из решения граничной задачи Штурма
–
Лиувилля
k
00
(
µ
n
,
ξ
) +
µ
2
n
k
(
µ
n
,
ξ
) =
0;
(23)
k
0
¡
µ
n
,
ξ
1
¢
−
Bi
1
k
¡
µ
n
,
ξ
1
¢
=
0;
(24)
k
0
¡
µ
n
,
ξ
2
¢
+
Bi
2
k
¡
µ
n
,
ξ
2
¢
=
0
,
(25)
где
ξ
1
=
0
и
ξ
2
=
1.
Решая уравнение
(23)
совместно с граничным условием
(24),
нахо
-
дим ненормированное ядро интегрального преобразования
.
С точно
-
стью до постоянной интегрирования решение имеет вид
k
(
µ
n
,
ξ
) =
cos
(
µ
n
ξ
) +
Bi
1
µ
n
sin
(
µ
n
ξ
)
.
(
26
)
Нормирование ядра
k
(
µ
n
,
ξ
)
проводится в соответствии с формулой
k
(
µ
n
,
ξ
) =
k
(
µ
n
,
ξ
)
√
N
,
(
27
)
где
N
=
1
Z
0
k
2
(
µ
n
,
ξ
)
d
ξ
=
1
Z
0
·
cos
(
µ
n
ξ
) +
Bi
1
µ
n
sin
(
µ
n
ξ
)
¸
2
d
ξ
=
=
1
2
"
1
+
sin2
µ
n
2
µ
n
+
µ
Bi
1
µ
n
¶
2
µ
1
−
sin2
µ
n
2
µ
n
+
2
Bi
1
sin
2
µ
n
¶ #
.
(28)
Характеристическое уравнение для определения собственных чи
-
сел задачи Штурма
–
Лиувилля получается в результате подстановки ре
-
шения
(26)
в граничное условие
(25):
ctg
µ
n
=
µ
2
n
−
Bi
1
·
Bi
2
µ
n
¡
Bi
1
+
Bi
2
¢
.
(
29
)
Функции
f
и
θ
∗
(
0
)
в правой части начального условия
(20)
находят из
выражений
:
6 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2003.
№
4