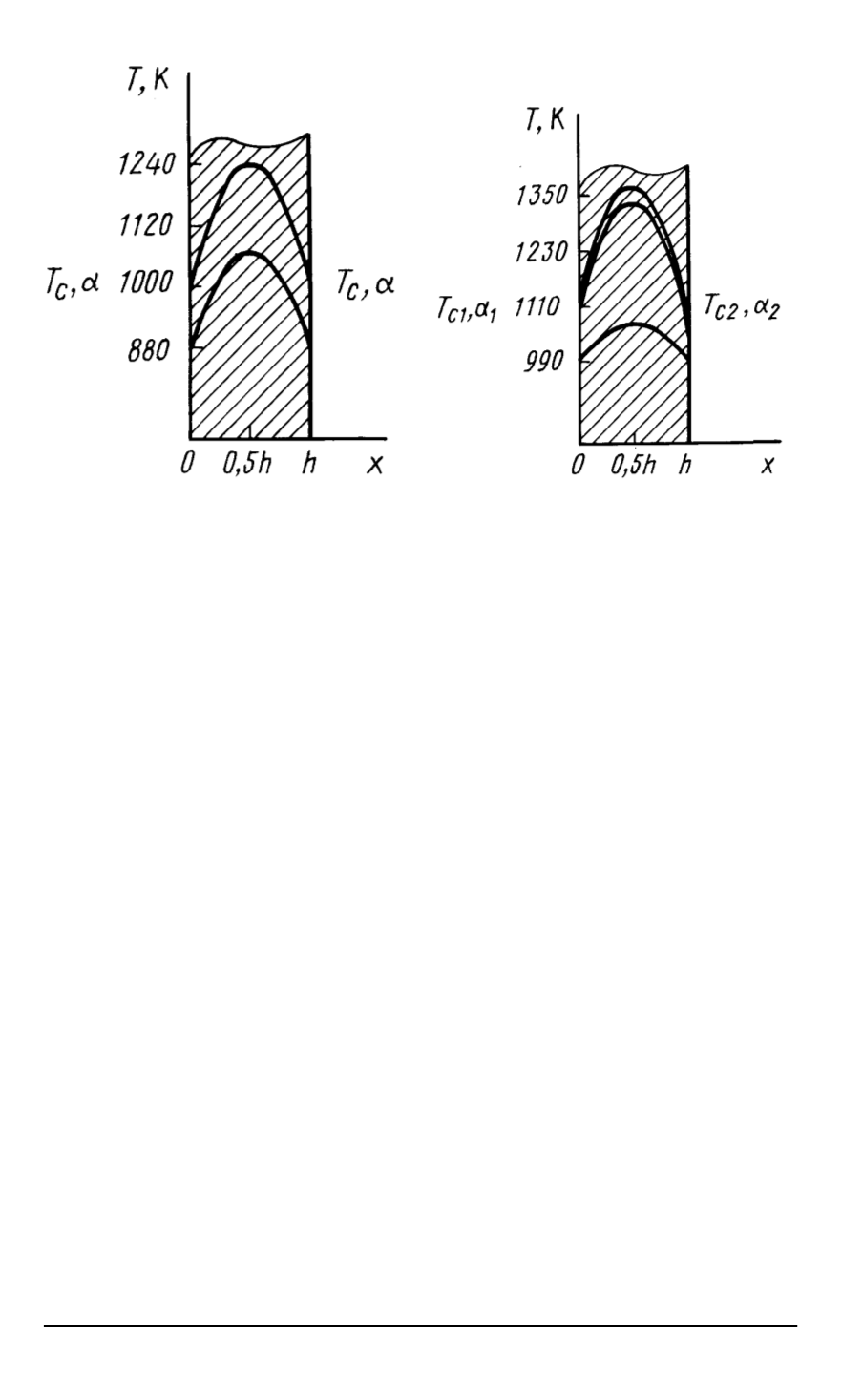
Рис
. 5.
Распределение температуры в
пластине при условиии симметрично
-
го нагрева
:
T
c1
=
T
c2
=
T
c
=
673
К
,
коэффициент теп
-
лоотдачи
α
1
=
α
2
=
α
=
4
·
10
3
Вт
/(
м
2
·
К
),
q
v
6
=
0 (p
исунок отражает изменение тем
-
пературы по пластине через
12
с и
72
с
после начала нагрева
)
Рис
. 6.
Распределение температуры в
пластине с
q
v
6
=
0
,
разделяющей среду
на две части
(
см
.
подпись к рис
. 4)
С целью исследования сходимости полученного решения было
проанализировано распределение температуры по толщине пластины
(
формула
(38))
для материалов с существенно различными свойствами
.
1.
Материал со следующими теплофизическими свойствами
:
ρ
=
=
1750
кг
/
м
3
,
c
=
700
Дж
/(
кг
·
K),
λ
=
23
Вт
/(
м
·
K).
2.
Медь
,
для которой
ρ
=
8728
кг
/
м
3
,
c
=
425
,
1
Дж
/(
кг
·
К
),
λ
=
=
388
Вт
/(
м
·
К
).
3. B
исмут
,
для которого
ρ
=
9560
кг
/
м
3
,
c
=
134
,
6
Дж
/(
кг
·
К
),
λ
=
=
13
,
5
Вт
/(
м
·
К
).
Условия
,
общие для всех трех вариантов
, —
это граничные усло
-
вия
(
см
. 1-
й вариант расчета
),
а начальное
—
температура пластины
T
0
=
300
К
.
Для приведенных условий было определено количество
членов ряда в правой части формулы
(38),
достаточное для получения
результата
,
отличающегося от точного не более чем на
1 %.
Результаты
исследования для
1, 2
и
3-
го материалов соответственно приведены на
рис
. 7,
a,
б
и
в
соответственно
.
Вертикальные черточки на рис
. 7
а
–
в
—
это интервалы значений
числа Фурье
,
для которого при соответствующем числе членов ряда
ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2003.
№
4 13


