+
1
µ
2
n
+
(
Bi
−
2
)
sin
µ
n
µ
3
n
+
2Bi cos
µ
n
µ
4
n
−
2Bi
µ
4
n
¶ #
×
×
Ã
cos
µ
µ
n
x
h
¶
+
Bi
µ
n
sin
µ
µ
n
x
h
¶ !
.
Этому решению соответствует рис
. 5.
А для
2-
го варианта
,
если
q
v
6
=
0,
решение получается на основе формулы
(38) (
рис
. 6).
Метод конечных интегральных преобразований
,
использованный
при решении задачи
,
имеет ряд существенных преимуществ перед
методом Фурье
,
которым также пользуются для решения задач этого
же класса
.
Наиболее существенными достоинствами можно считать
простоту получения решений и возможность применения метода к од
-
нородным и неоднородным краевым задачам
.
Однако он применяется
только к линейным дифференциальным уравнениям с линейными гра
-
ничными условиями при решении задач теплопроводности для тел
канонической формы
.
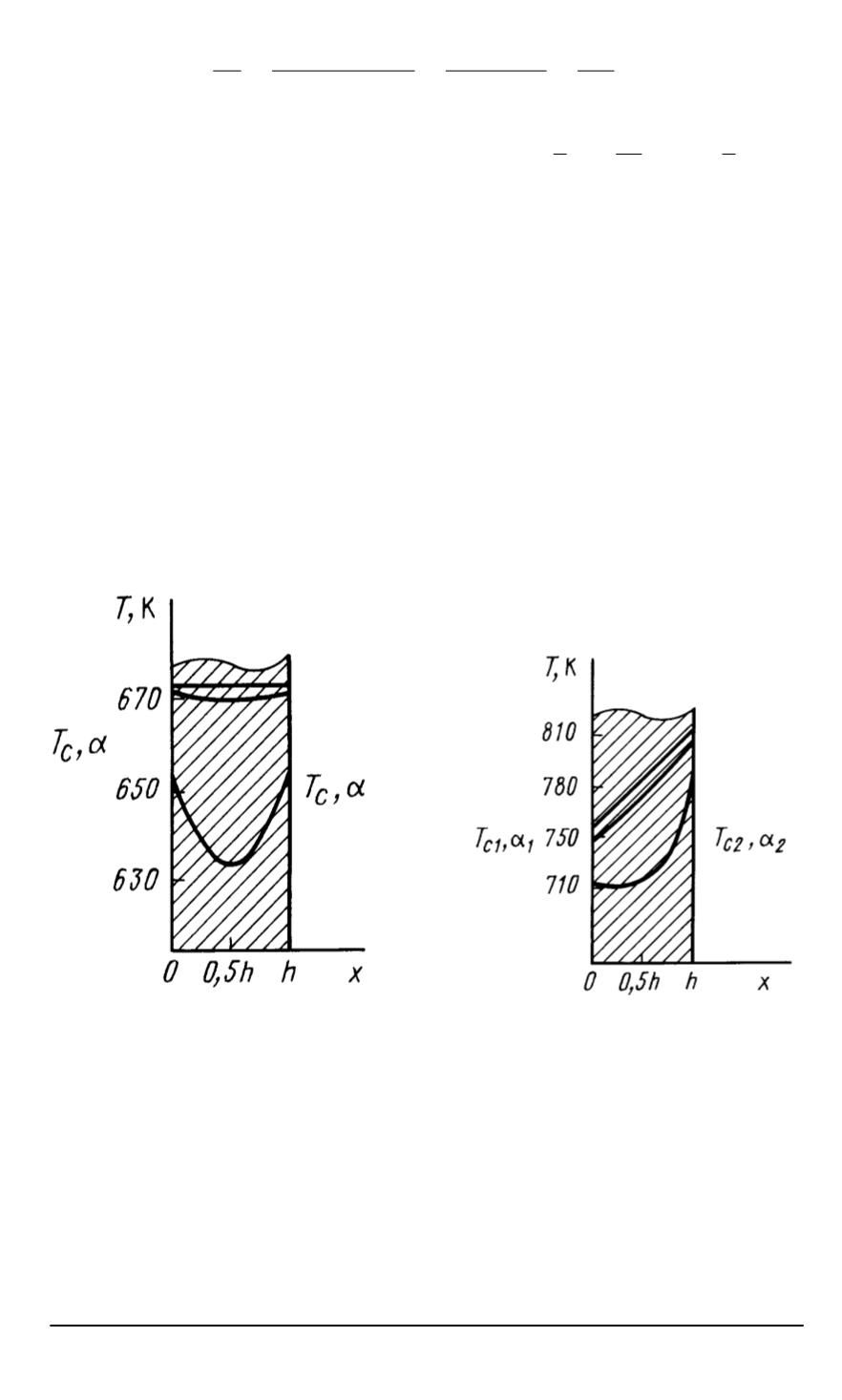
Рис
. 3.
Нагрев пластины
,
не
имеющей внутренних источников
теплоты
,
помещенной в среду с
температурой
T
c1
=
T
c2
=
T
c
=
673
К
и коэффициентом теплоотдачи
α
1
=
α
2
=
α
=
4
·
10
3
Вт
/(
м
2
·
К
)
(
линии на рисунке соответствуют
моментам времени
12
с
, 24
с
, 72
с
)
Рис
. 4.
Нагрев пластины
,
не име
-
ющей внутренних источников теп
-
лоты и разделяющей среду на две
части
:
одну
—
с коэффициентом
теплоотдачи
α
1
=
3
·
10
3
Вт
/(
м
2
·
К
)
и
температурой
T
c1
=
723
К и другую
—
с коэффициентом теплоотдачи
α
2
=
5
·
10
3
Вт
/(
м
2
·
К
)
и температу
-
рой
T
c2
=
823
К
(
зависимости даны
для моментов времени
12
с
, 24
с
,
72
с
)
12 ISSN 0236-3941.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Машиностроение
". 2003.
№
4


