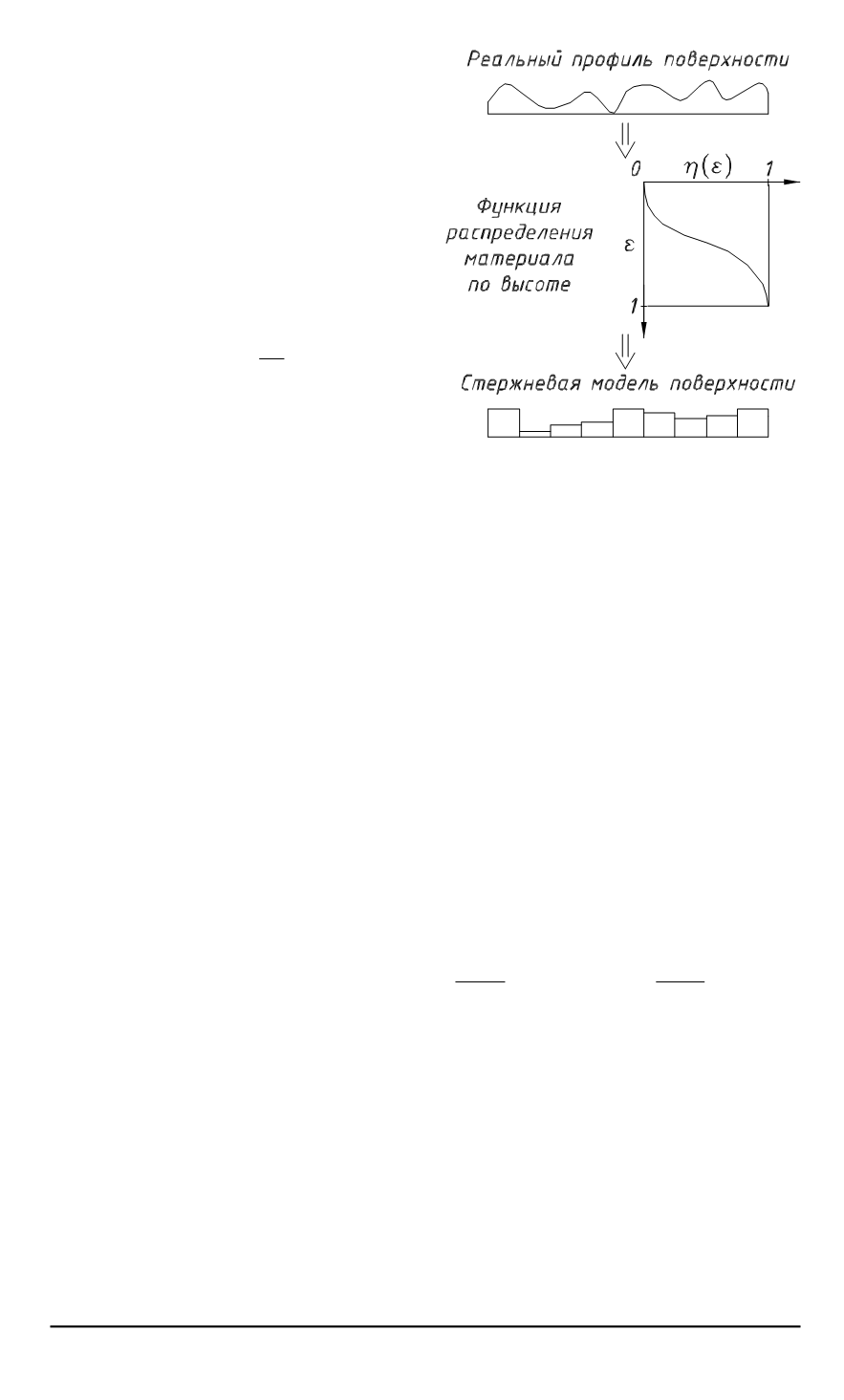
Рис. 2. Моделирование волнистых по-
верхностей
где
ε
— отношение расстояния меж-
ду вершиной самого высокого вы-
ступа и плоскостью измерения к
высоте самого высокого выступа,
A
ε
— сумма сечений выступов на
уровне
ε
,
A
н
— номинальная пло-
щадь;
Условие распределения вершин
ξ
имеет вид
ξ
(
ε
) =
n
ε
n
н
,
где
n
ε
— число контактирующих
выступов на уровне
ε
,
n
н
— общее
число выступов.
Функция распределения мате-
риала по высоте
η
и функция распределения вершин
ξ
определяют-
ся на основе обработки профилограмм. Для стержневой модели —
η
(
ε
)
≡
ξ
(
ε
)
.
Наилучшая аппроксимация функции распределения материала по
высоте
η
получается с использованием бета-распределения [2]:
η
(
υ, ψ, ε
) =
ω
ε
Z
0
x
υ
−
1
(1
−
x
)
ψ
−
1
dx ,
где
υ
,
ψ
— параметры бета-распределения;
ω
— коэффициент, который
определяется из условия
η
(
υ, ψ,
1) = 1
.
Если профиль поверхности близок к синусоидальному, то такую
поверхность можно описать следующим уравнением [5]:
w
(
x, y
) = Δ
1
+ Δ
2
−
Δ
1
cos
2
π x
H
1
−
Δ
2
cos
2
π y
H
2
,
(1)
где
Δ
1
и
Δ
2
— продольная и поперечная амплитуда волны;
H
1
и
H
2
—
продольный и поперечный шаг волны.
С помощью формулы (1) можно моделировать двумерную волни-
стость. Частным случаем двумерной волнистости является изотропная
волнистость, при которой
Δ
1
= Δ
2
и
H
1
=
H
2
. Одномерная волни-
стость является вырожденным случаем двумерной волнистости при
Δ
2
= 0
.
Таким образом, при описании топографии поверхности элемен-
та фрикционной пары можно допустить, что поверхность трения не
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2006. № 1 87


