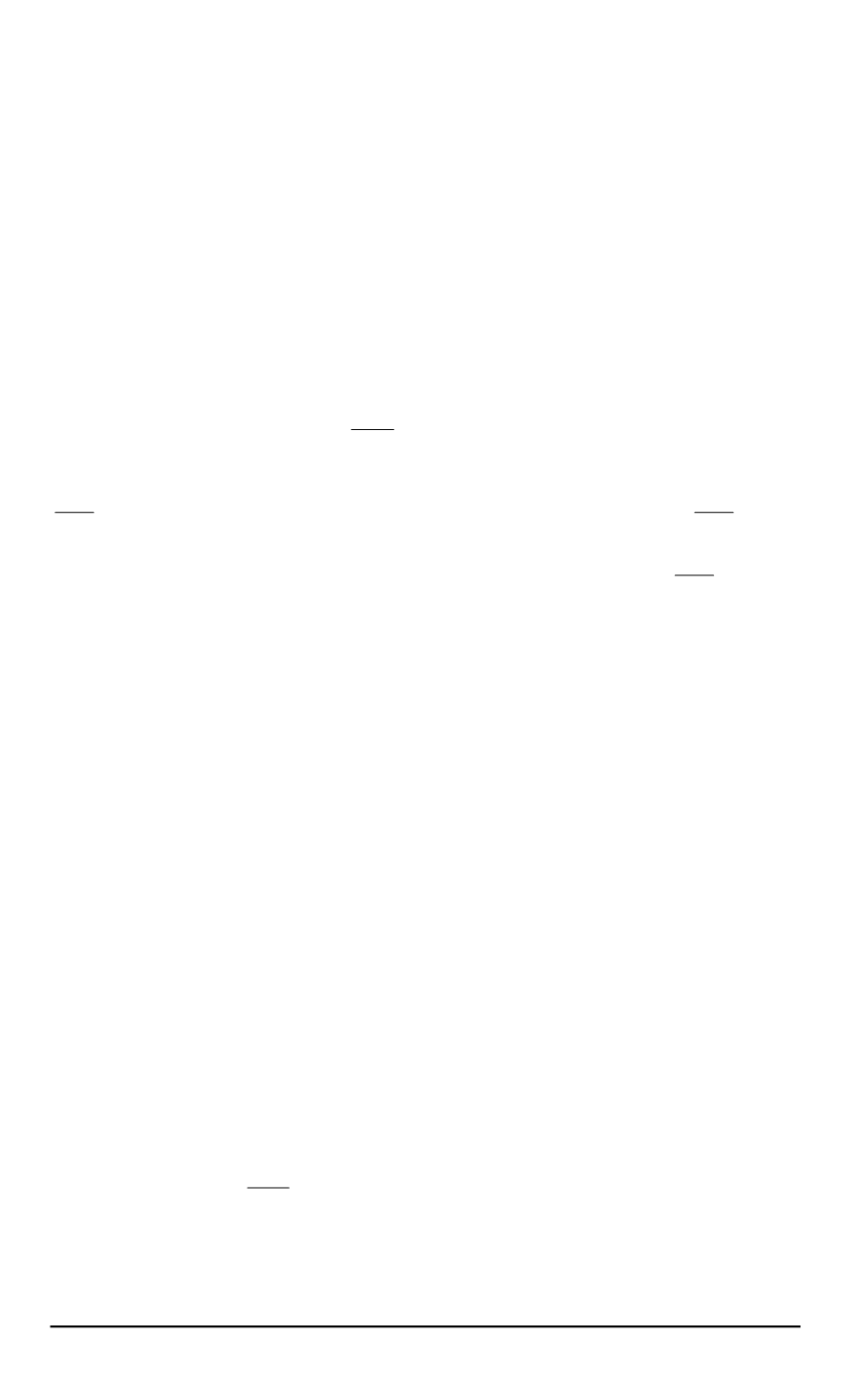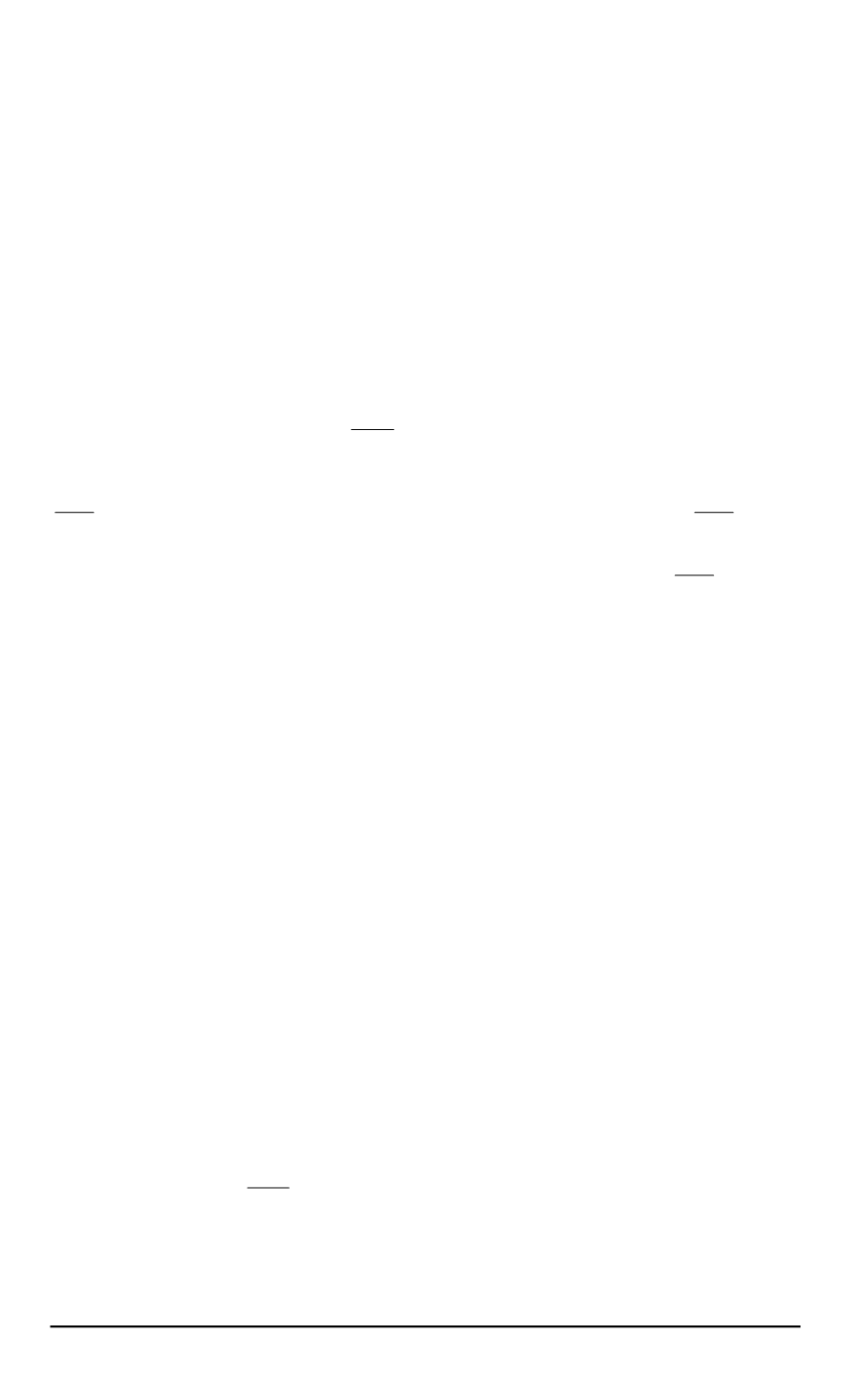
где
c
и
λ
— теплоемкость накладки и теплопроводность накладки;
c
д
,
λ
д
и
ρ
д
— теплоемкость, теплопроводность и плотность диска соответ-
ственно.
Экспериментальные исследования по определению термической
проводимости контакта
α
к
для фрикционных пар ФПМ–сталь, чугун
приведены в работе [8].
Тепловая подмодель.
Тормозная накладка.
В качестве исходных
переменных примем плотность
q
н
теплового потока, поступающего
в накладку, а определяемых переменных — температуру тормозной
накладки
T
н
.
Задача определения
T
н
сводится к решению уравнения теплопро-
водности [9]:
∂ T
н
∂ t
=
a
Δ
T
н
,
со следующими граничными условиями: в случае теплоизоляции —
∂T
н
∂n
Γ
= 0
; в случае теплоотдачи по закону Ньютона —
−
λ
∂T
н
∂n
Γ
=
=
σ
(
T
н
−
T
e
)
; в случае поступления теплового потока —
λ
∂T
н
∂n
Γ
=
q
н
,
и начальным условием —
T
н
|
t
=0
=
T
e
, где
a
— температуропровод-
ность;
σ
— коэффициент теплоотдачи [20];
T
e
— температура окружа-
ющей среды;
Δ
— оператор Лапласа;
Γ
— граничная поверхность;
n
—
нормаль к граничной поверхности.
Тормозной диск.
Исходные переменные — плотность
q
д
теплового
потока, поступающего в диск, определяемые переменные — темпера-
тура тормозного диска
T
д
.
Материалы тормозных дисков (сталь, чугун) имеют высокую тем-
пературопроводность, что приводит к быстрому выравниванию тем-
пературы тела по всему объему. Поэтому примем допущение, что тем-
пература диска во всех точках одинакова (это позволит значительно
упростить задачу).
Изменение внутренней энергии диска можно представить как
dQ
д
=
c
д
m
д
dT
д
,
(6)
где
m
д
— масса диска.
С другой стороны, на основании закона сохранения энергии можно
записать равенство
dQ
д
dt
=
Z
A
q
д
dA
−
σ
д
A
д
(
T
д
−
T
e
)
,
(7)
где
σ
д
— коэффициент теплоотдачи диска [20],
A
— поверхность трения
накладки,
A
д
— поверхность охлаждения диска.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2006. № 1 93