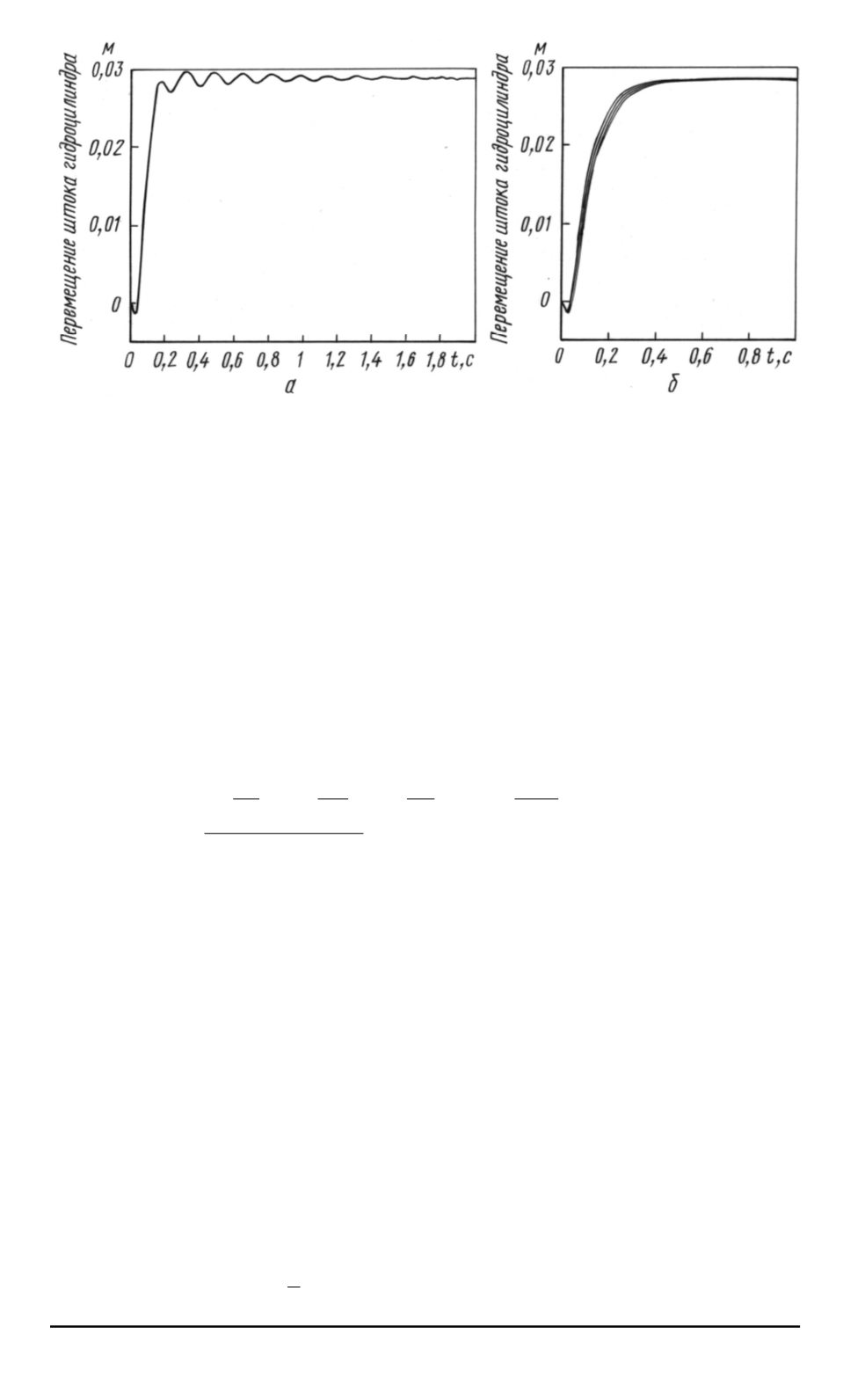
Рис. 6. Переходные характеристики нелинейного ЭГСП в случае симметрично-
го гидроцилиндра:
а
— без регулятора;
б
— с эталонной моделью и регулятором
без дополнительного регулятора. Вследствие чего задача устойчиво-
сти была решена вторым методом Ляпунова. Одновременно для рас-
чета коэффициентов регулятора была использована эталонная модель,
которая принята в системе управления ЭГСП с нелинейными характе-
ристиками, чтобы обеспечивать переходные характеристики, близкие
к эталонной модели. Приведенные нелинейные уравнения преобразо-
ваны следующим образом:
x
1
=
y, x
2
= ˙
y, x
3
=
p
н
, x
4
=
x
з
, x
5
= ˙
x
4
;
˙
x
1
=
x
2
; ˙
x
2
=
F
ц
m
x
3
−
к
тр
m
x
2
−
P
f
m
; ˙
x
3
=
2
B
ж
V
0
(
Q
з
−
F
ц
x
2
−
C
y
x
3
);
Q
з
=
к
0
з
x
4
p
p
п
−
х
3
sign(
x
4
); ˙
x
4
=
x
5
;
˙
x
5
=
−
ω
2
ЭГУ
x
4
−
2
ς
ЭГУ
ω
ЭГУ
x
5
+
К
х
u
ω
2
ЭГУ
u.
Используя эти уравнения, можно найти функцию Ляпунова, запи-
санную для ошибки
e
i
между переменами
x
i
состояния реальной си-
стемы и переменами
x
ei
состояния эталонной модели. Предварительно
полезно построить структурную схему реальной системы ЭГСП и эта-
лонной модели вместе (рис. 7). Согласно этой схеме получается сигнал
ошибки, в соответствии с которой регулятор обеспечивает выполнение
критерия [4, 9]
lim
t
→∞
e
i
(
t
) = 0
при
e
i
=
x
i
−
x
ei
, где
i
= 1
. . .
5
.
Функцию Ляпунова выбирают в форме, используемой в критерии
оптимизации.
При
i
= 1
V
1
=
1
2
e
2
1
;
V
1
>
0
, когда
e
1
6
= 0
. Для устойчивости
106 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2007. № 1


