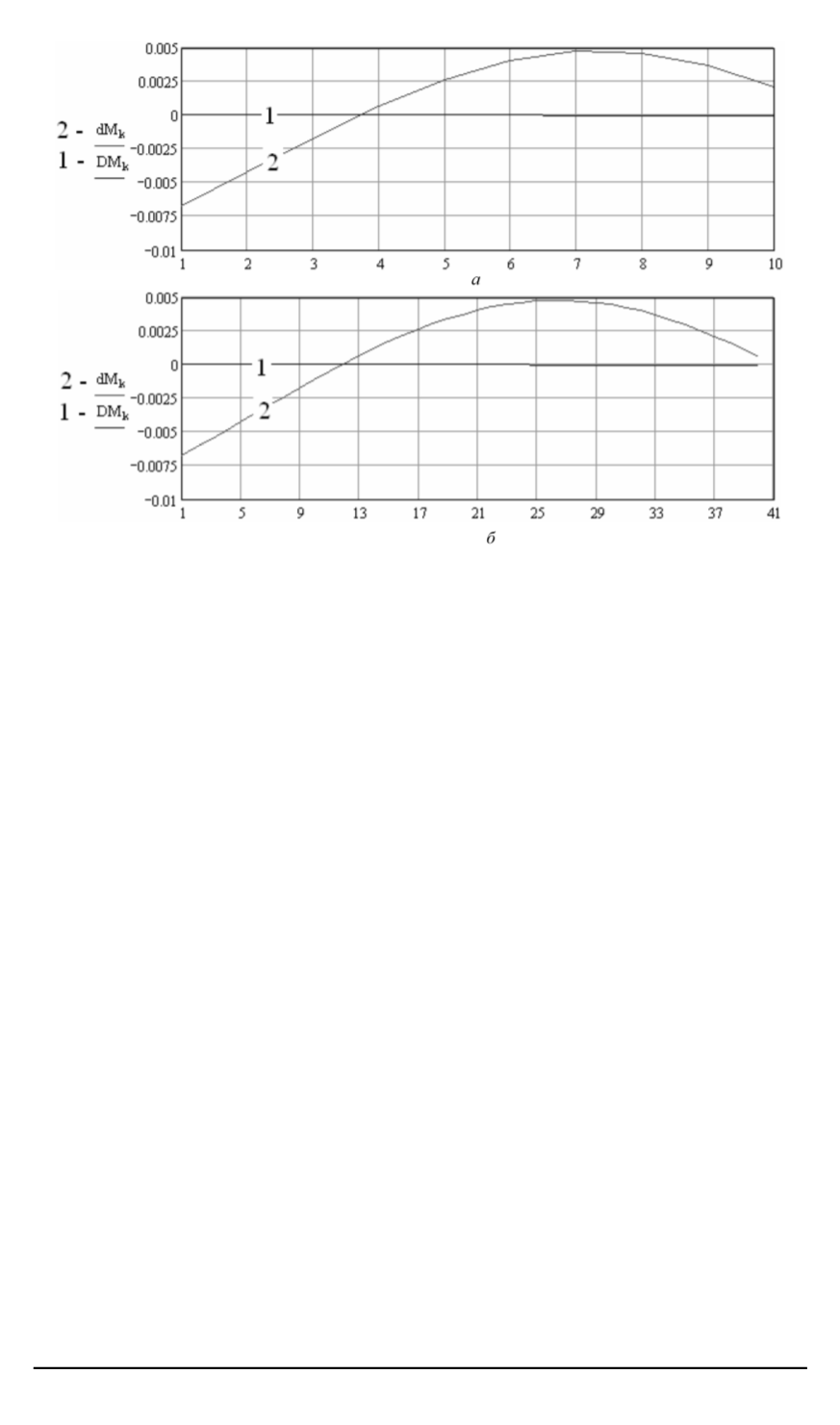
Рис. 12. Сглаженное развитие погрешностей расчета с использованием ком-
плекса ANSYS (кривые
2
) и предлагаемй методики (кривые
1
) для десяти (
а
) и
сорока (
б
) КЭ
А1 соответствует решению задачи методом сопротивления материа-
лов (эталонному), а матрица А2 получена по предлагаемой методике
согласно приведенным искусственным ограничениям.
На рис. 12,
а
показано (сглаженное для иллюстративности) разви-
тие погрешностей согласно рис. 11,
б
при использовании чебышевской
нормы. На этом и последующих рисунках кривая
1
соответствует ре-
зультатам, полученным по методике, приведенной в данной работе, в
условиях искусственного ограничения точности представления истин-
ных результатов, а кривая
2
соответствует расчетам, выполненным с
помощью комплекса ANSYS.
Казалось бы, погрешность расчета по методике настоящей работы
равна нулю. Конечно, в условиях искусственного ограничения точно-
сти это не так. Графики (см. рис. 12,
а
) показывают лишь наглядно,
что при десяти КЭ комплекс ANSYS на несколько порядков увеличи-
вает погрешность расчета. Безусловно, в приведенном примере дана
модельная ситуация, но именно она и возможна при проведении рас-
четов сложных конструкций, где нет эталонной базы расчетов, а ма-
лые погрешности расчета приводят подобно неправильно заданным
начальным значениям к непредсказуемым эффектам и результатам.
Поэтому на рис. 13 показано развитие погрешностей (см. рис. 12,
а
)
только для расчета, выполненного по методике, предлагаемой в насто-
ящей работе.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 3 25


