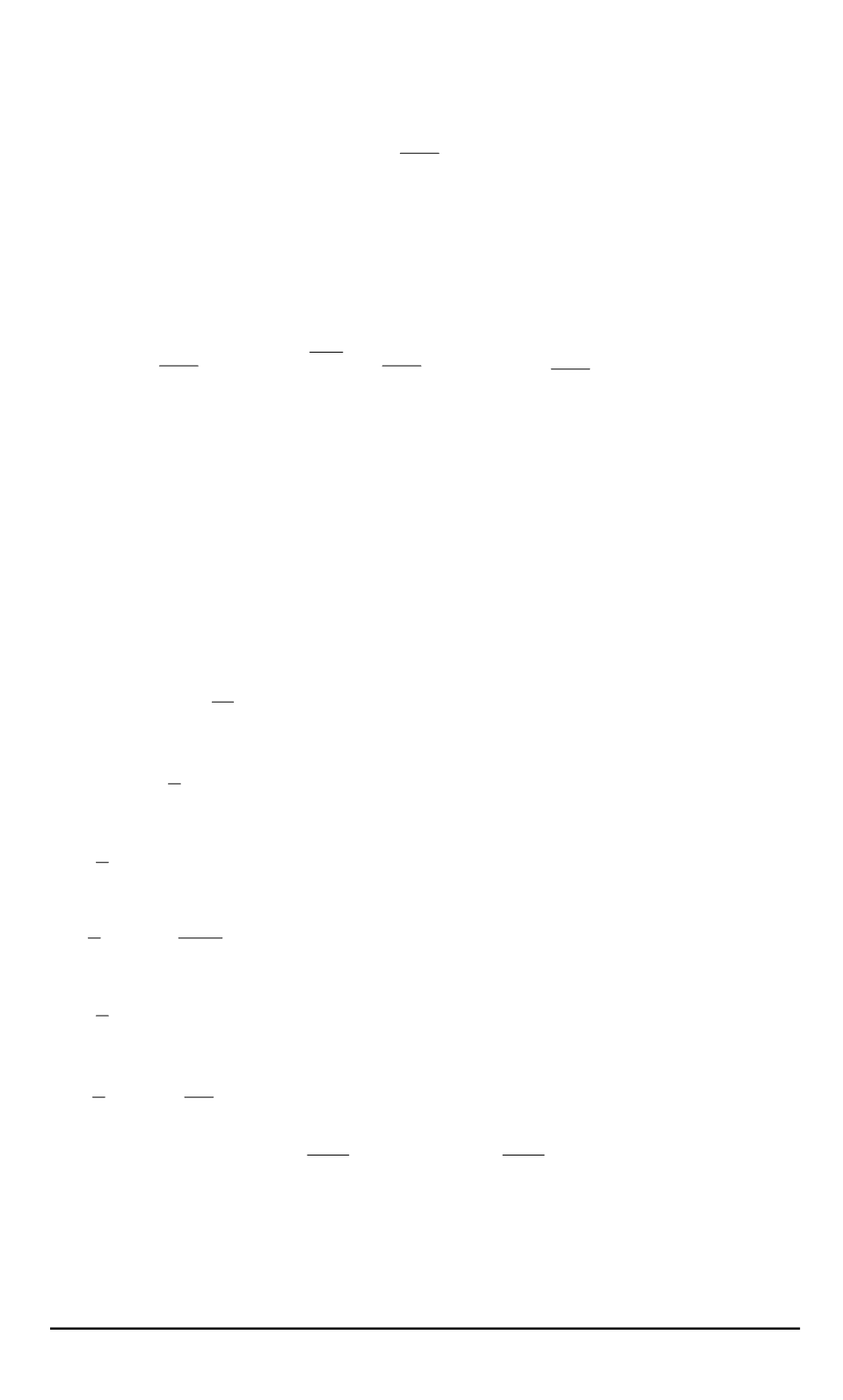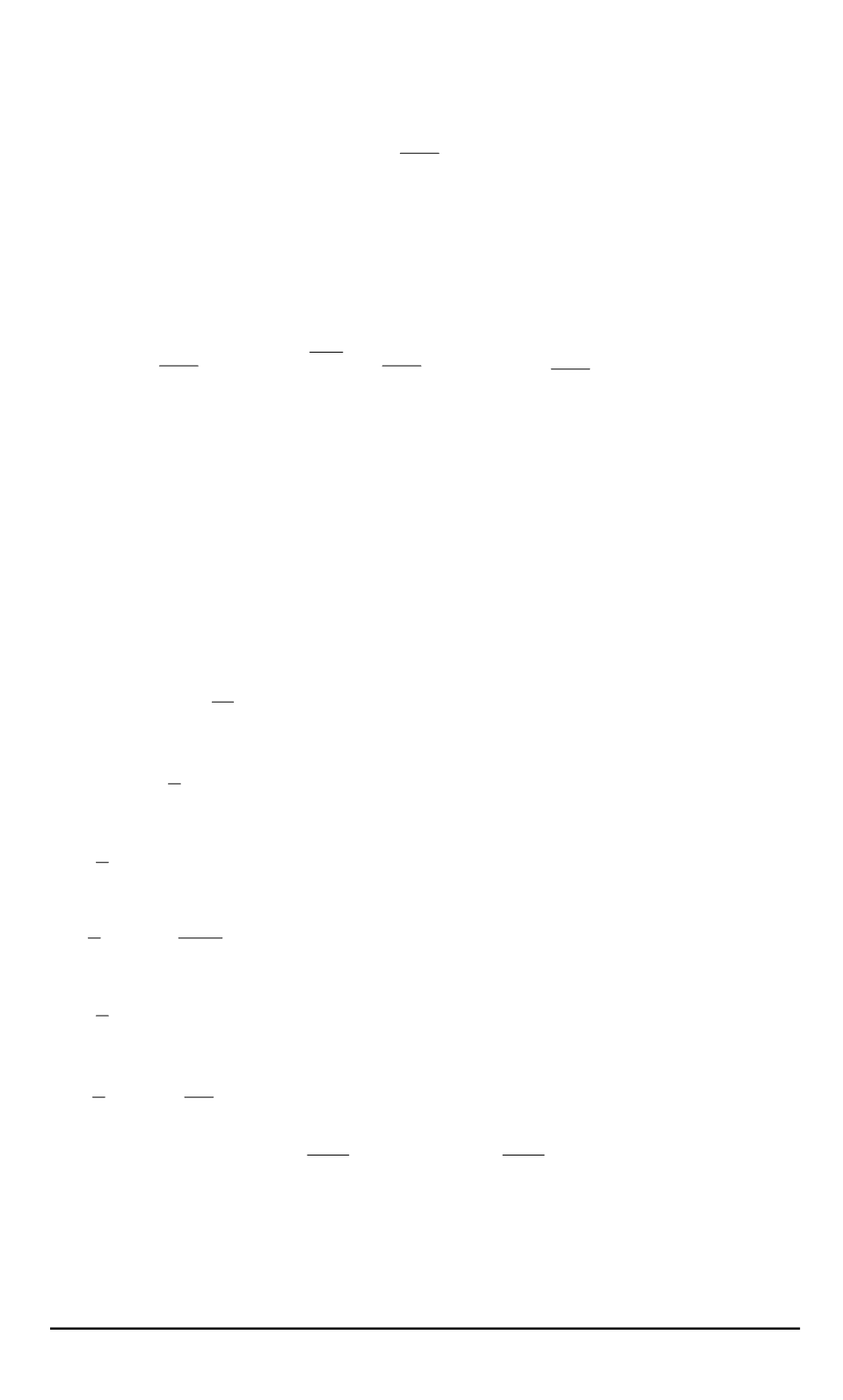
которые необходимо дополнить граничным кинематическим условием
на смачиваемой поверхности
S
оболочки
w
0
=
∂φ
∂n
0
на
S
(16)
и силовыми условиями взаимодействия оболочки с жидкостью, кото-
рые с учетом формул (12) и (16) и выводов (1)–(3) можно записать в
виде
L
(
u
0
∂φ
∂n
0
)
+
ρ
0
h
0
∂
2
∂t
2
(
0
∂φ
∂n
0
)
=
0
−
ρ
∂
2
φ
∂t
2
!
на
S,
(17)
где
L
=
{
L
jk
}
2
j,k
=1
— самосопряженный оператор теории тонких обо-
лочек, а
f
k
(
x, t
)
,
k
= 1
,
2
, в уравнениях (14) и (15) — заданные внешние
воздействия.
Закон изменения энергии.
Умножим динамические граничные
условия (14), (15) и (17) на
ρ
( ˙
w
Г
)
, ρ
( ˙
w
Σ
)
и
˙ˉ
U
соответственно и про-
интегрируем по поверхностям
Г
0
,
Σ
и
S
. Суммируя полученные ре-
зультаты и учитывая кинематическое условие (16), после несложных
преобразований получим выражение
d
dt
(
T
ж
+
T
об
+
П
ж
+
П
об
) =
−
2Φ +
A
(
e
)
,
(18)
где
T
ж
=
1
2
ρ
Z
Q
(
r
˙
φ
)
2
dQ
— кинетическая энергия жидкости;
T
об
=
=
1
2
ρ
0
h
0
Z
S
(
˙
~U
0
)
2
dS
— кинетическая энергия оболочки;
П
ж
=
=
1
2
Z
Г
0
ρg
∂φ
∂n
Г
2
d
Г
0
— потенциальная энергия жидкости;
П
об
=
=
1
2
Z
S
(
L
1
/
2
˙ˉ
U
0
)
2
dS
— потенциальная энергия оболочки;
Φ =
=
1
2
γρ
Z
∂
˙
φ
∂n
2
d
Σ
— диссипативная функция малых движений
жидкости;
A
(0)
=
Z
Г
0
f
1
∂w
1
∂t
2
d
Г
0
+
Z
Σ
f
2
∂w
3
∂t
2
d
Σ
— работа внешних
воздействий на жидкость.
Закон изменения энергии показывает, что в расматриваемой меха-
нической системе работа внешних воздействий лишь частично расхо-
дуется на изменение полной механической энергии.
50 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 1