
В.Н. Елисеев, В.А. Товстоног, Т.В. Боровкова
116
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 1
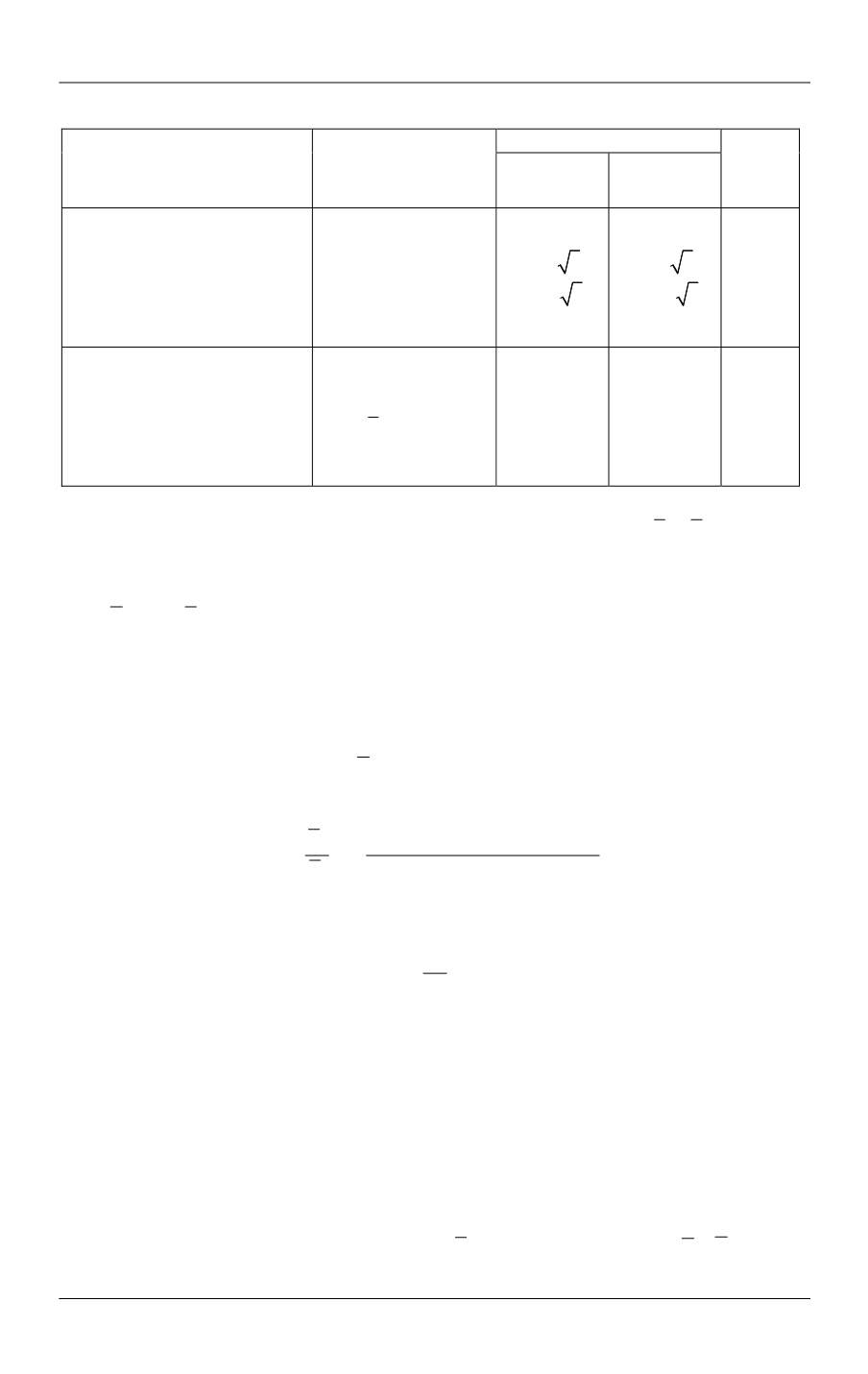
Окончание табл. 1
Форма тела и коэффициенты
в уравнении (17)
Уравнение для ядра
преобразования
λ, ξ
K
Функция
При-
меча-
ние
ψ μ , ξ
n
ψ μ , ξ
n
Ребро треугольного и тра-
пециевидного поперечно-
го сечения с малым углом
при вершине:
ρ 1,
ξ,
p
2 2
2
2
( ) , ω μ ( )
q ml
ml
2
ξ
ω 0
K K K
0
(2ω ξ ),
J
0
(2ω ξ )
I
0
(2ω ξ ),
Y
0
(2ω ξ )
K
2
ω 0,
2
ω 0
Круглое ребро постоянной
толщины:
ρ ξ,
ξ,
p
2
ξ( ) ,
q ml
ω
2
= μ
2
— (
ml
)
2
2
1 ω 0
ξ
K K K
0
μξ ,
J
0
μξ
I
0
ωξ ,
Y
0
ωξ
K
2
ω 0,
2
ω 0
В выражении (21) содержится три неизвестные величины
1
,
B
2
B
и
μ ,
n
для
определения которых имеются только два граничных условия (18) и (19).
Для устранения этого затруднения поделим обе части (21) на одну из постоян-
ных
1
B
или
2
B
и определим ненормированное ядро интегрального преобразова-
ния
μ , ξ
n
K
с точностью до постоянной интегрирования. Основанием для такого
шага служит то, что в решении рассматриваемой задачи используется только нор-
мированное ядро, а процедура нормирования позволяет исключить его зависи-
мость от точности определения ненормированного ядра (формулы (9) и (10)).
Поделив обе части (21) на
1
B
и используя условия (18) и (19), находим зна-
чение константы
1
1
1
1
2
2
1
1
1
1
1
ψ μ , ξ β μ , ξ
,
φ μ , ξ β φ μ , ξ
n
n
n
n
B B
B
(22)
а также характеристическое уравнение для определения собственных чисел
2
2
2
2
2
2
2
2
2
1
φ μ , ξ β φ μ , ξ
β ψ μ , ξ
ψ μ , ξ .
n
n
n
n
B
(23)
Соотношение для определения ненормированного ядра принимает вид
2
μ , ξ ψ μ , ξ
φ μ , ξ .
n
n
n
K
B
(24)
Из выражения (8) находим весовую функцию
ρ ξ ,
а из табл. 1 или спра-
вочника по обыкновенным дифференциальным уравнениям — функции
ψ μ , ξ
n
и
φ μ , ξ .
n
Используя далее последовательно формулы (22)–(24), (10), (9), (20), (13)–(16)
и (11), (12), находим
2
,
B
μ ,
n
μ , ξ ,
n
K
,
N
μ , ξ ,
n
K
1
ξ , ,
p P
2
P
и
,
F
.
f
















