
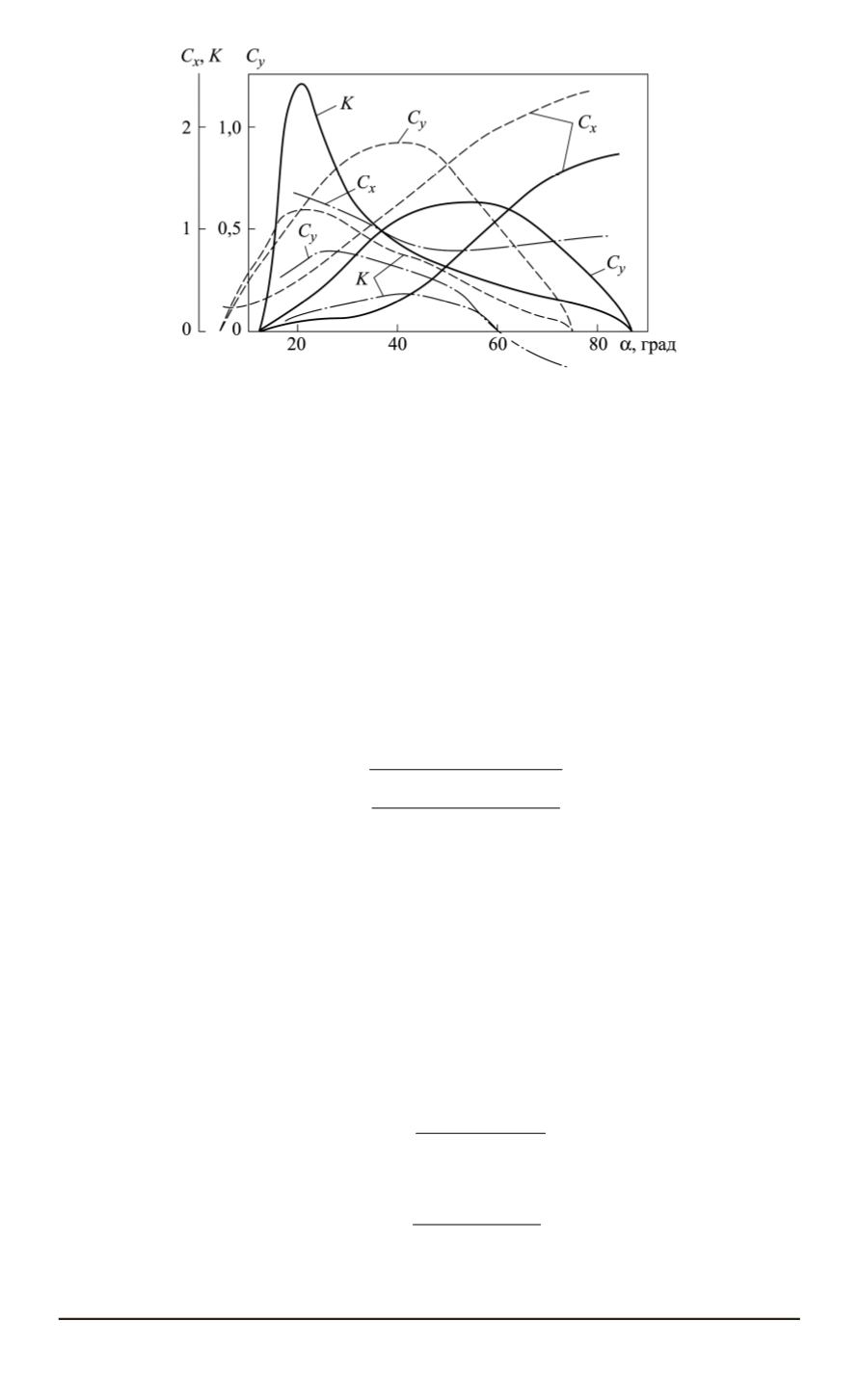
Рис. 1. Зависимости коэффициентов лобового сопротивления
C
x
, подъемной
силы
C
y
и аэродинамического качества
K
от угла атаки
α
(
M >
4
)
:
——— — космический самолет с
K
max
= 2
,
4
; – – – — КА типа “несущий корпус” с
K
max
= 1
,
5
; –
∙
–
∙
– — КА скользящего типа с
K
max
= 0
,
34
В конечной точке траектории
t
=
t
к
(вылет КА из атмосферы)
известно значение высоты полета
h
(
t
к
) =
h
атм
или радиуса-вектора
КА
r
(
t
к
)
:
r
(
t
к
) =
r
к
=
R
+
h
атм
;
(4)
здесь
h
атм
= 100
км — высота условной границы атмосферы Марса.
При выведении на орбиту ИСМ с заданным радиусом апоцентра
r
α
должно выполняться соотношение, связывающее значения конечных
параметров
V
к
,
θ
к
и
r
к
:
V
к
=
s
2
μr
α
(
r
α
−
r
к
)
r
к
(
r
2
α
−
r
2
к
cos
2
θ
к
)
.
(5)
В качестве критерия оптимальности использовался максимум ско-
рости КА в конечной точке траекторий
J
=
V
к
= max
,
что обеспе-
чивает минимум потребных энергозатрат при формировании орбиты
ИСМ [5, 15].
Задача максимизации коридора входа КА в атмосферу сводится к
решению двух независимых вариационных задач о нахождении ми-
нимума и максимума высот условного перицентра, характеризующих
верхнюю и нижнюю границы коридора входа:
min
h
H
π
= min
r
2
0
V
2
0
cos
2
θ
H
0
μ
(
e
+ 1)
−
R
или
min
h
B
π
= max
r
2
0
V
2
0
cos
2
θ
B
0
μ
(
e
+ 1)
−
R ,
где
е
— эксцентриситет подлетной орбиты.
8 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2015. № 6
















