Модель расхода энергии силового агрегата с ДВС

2 / 11

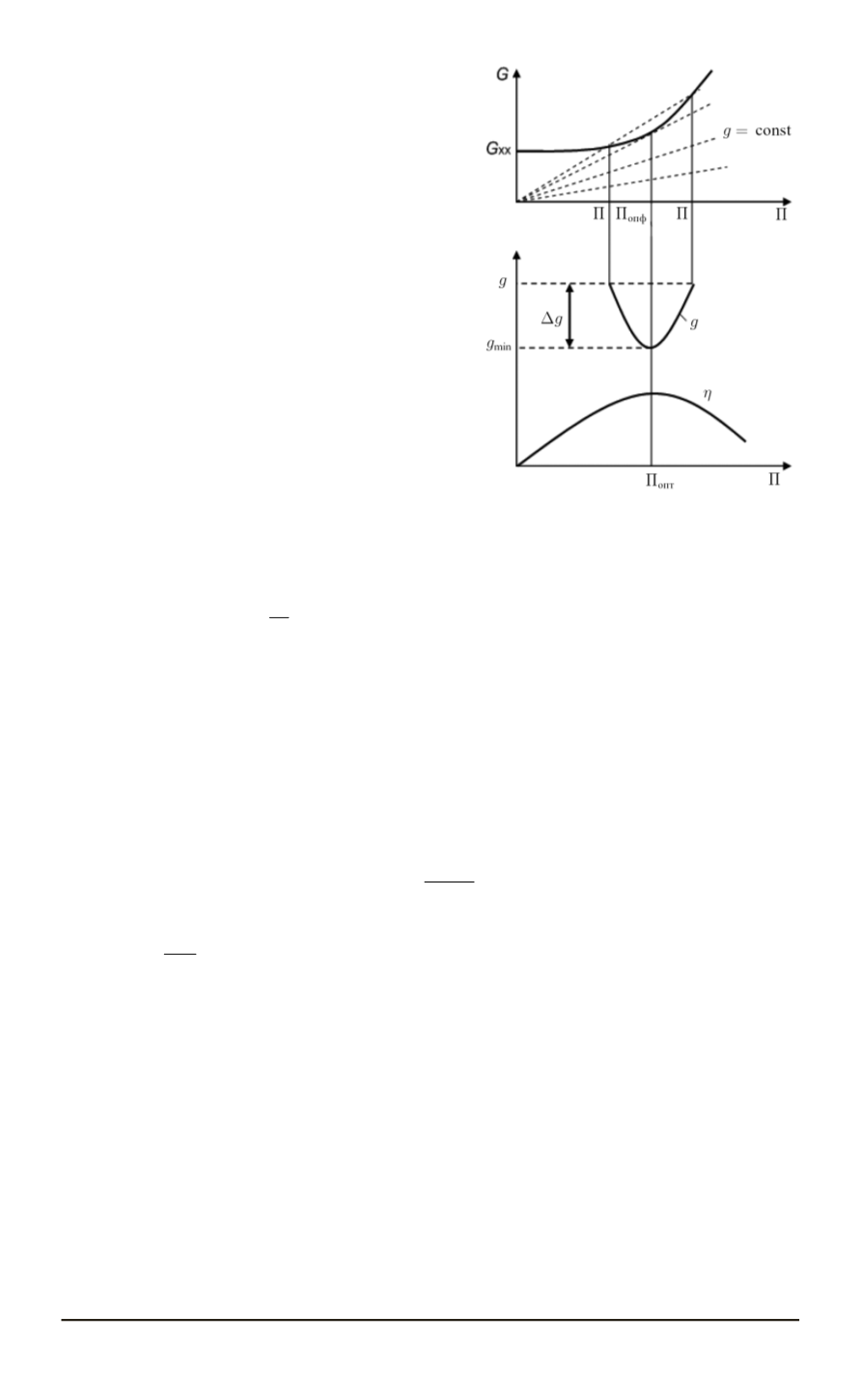
Рис. 1. Зависимости КПД абсолют-
ного часового G = f (Π) и удель-
ного g = f (Π) расходов энергии от
производительности машины
Особую сложность представляет про-
ектирование машин с дизельным дви-
гателем, оборудованным системой ав-
томатического регулирования скоро-
сти (САРС), так как двигатель это-
го типа может развивать одинаковую
мощность при различных сочетаниях
скоростного и нагрузочного режимов.
В связи с этим для снижения расхо-
да топлива на переходных режимах
в условиях эксплуатации необходи-
мо использовать математическую мо-
дель алгоритма управления двигате-
лем внутреннего сгорания (ДВС) по
экономической характеристике.
Экономичность расхода энергии
машины часто оценивается критери-
ем в удельных единицах
g =
G
Π
,
где П — производительность машины (выработка продукции в единицу
времени); G = f (П ) — часовой расход энергии.
При нулевой производительности П = 0 удельный расход энергии
бесконечно велик у машин любого типа, что делает эту оценку не-
удобной для инженерных расчетов (рис. 1). Поэтому ее часто заменя-
ют оценкой КПД. Например, для ДВС [1] эффективный КПД можно
рассчитать по формуле
η =
3600
Qнge
,
где ge =
G
W e
— удельный расход топлива ДВС, который показывает,
какое количество топлива расходует ДВС на единицу эффективной
мощности W e в течение часа; Qн — низшая теплота сгорания топлива.
Зависимость удельного расхода энергии g = f (Π) получается пе-
рестроением зависимости абсолютного расхода G = f (Π). Она имеет
минимум при оптимальной производительности Πопт, которая может
быть получена как абcцисса точки касания прямой, проведенной из
начала координат, к кривой G = f (Π) [2].
Характер изменения g = f (Π) объясняется тем, что увеличение
удельного расхода энергии левее минимума g = f (Π) происходит за
счет непропорционального увеличения удельных потерь энергии на
трение, а увеличение удельного расхода энергии правее оптимальной
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 5 107