
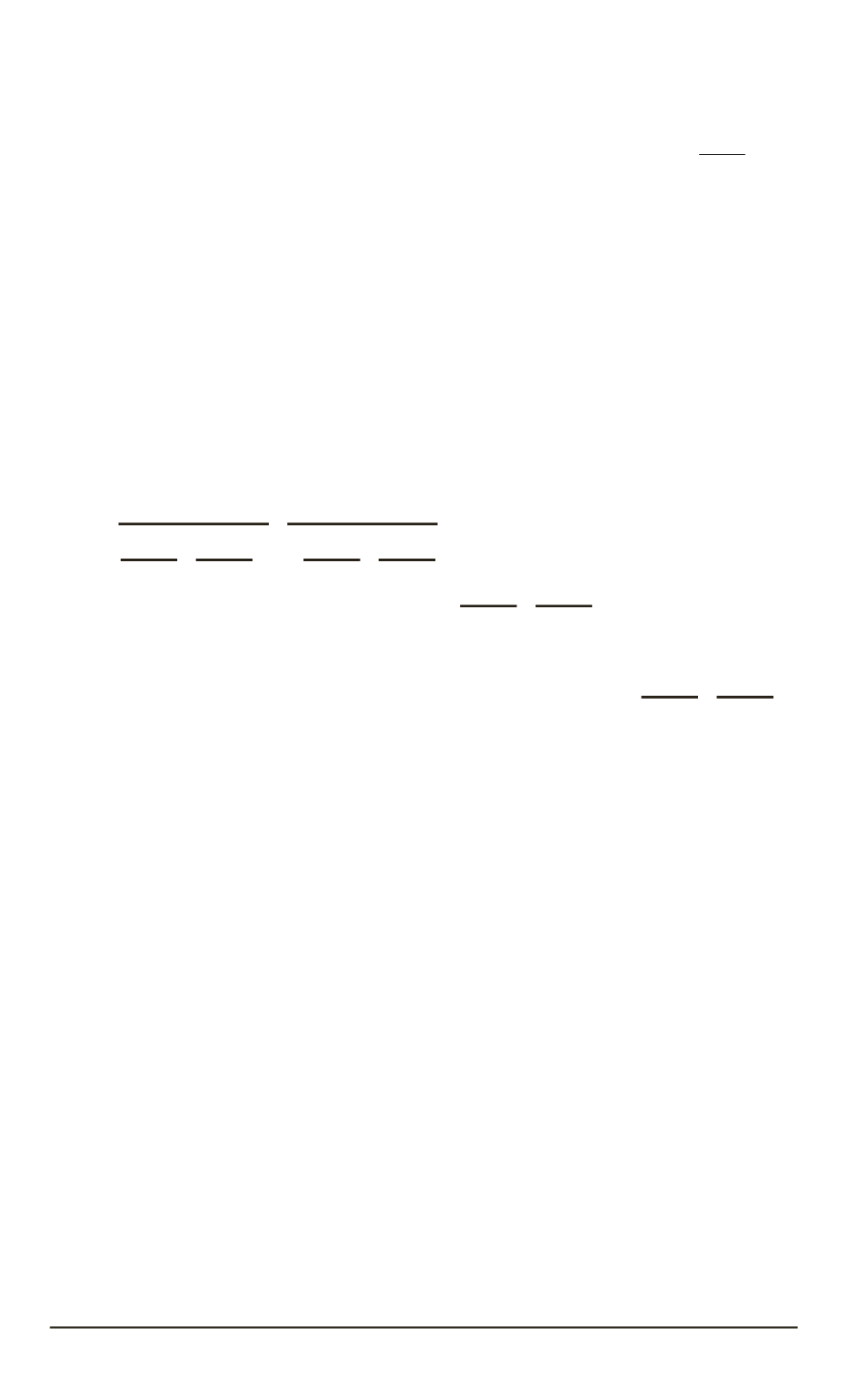
Ввиду ограниченности значения реактивного ускорения на каждом
подынтервале на компоненты вектора
Δ
V
накладывается ограничение
по амплитуде
U
=
n
ΔV : Δ
V
(1)
j
+ Δ
V
(2)
j
+
∙ ∙ ∙
+ Δ
V
(
S
)
j
≤
Δ
V
j
max
, j
= 1
, K
o
.
(9)
Для задачи коррекции помимо терминальных условий может на-
кладываться дополнительное ограничение, касающееся работы дви-
гателя. Например, когда КА проходит через земную тень, корректи-
рующий двигатель не может работать. Кроме того, возможны и дру-
гие причины отключения двигателя на определенном участке полета.
Эти дополнительные ограничения по суммарной длительности работы
двигателя на некотором витке имеют вид
A
c
∙
ΔV
≤
b
,
(10)
где
A
c
=
1-й виток
z
}|
{
1
/a
max
∙ ∙ ∙
1
/a
max
|
{z
}
S
∙ ∙ ∙
1
/a
max
∙ ∙ ∙
1
/a
max
|
{z
}
S
2
−
й виток
z
}|
{
1
/a
max
∙ ∙ ∙
1
/a
max
. . .
R
−
й виток
z
}|
{
1
/a
max
∙ ∙ ∙
1
/a
max
— матрица размером
R
×
KS
, в каждой строке которой включаются все
подынтервалы на соответствующем витке;
R
— число витков. Вектор
ограничений
b
в этом случае равен
b =
Δ
t
1max
Δ
t
2max
...
Δ
t
R
max
.
Таким образом, исходная задача коррекции траектории (2), (4)–(6)
свелась к задаче математического программирования: найти вектор
Δ
V
, минимизирующий линейный функционал
I
[ΔV] = min
Δ
V
K
X
j
=1
S
X
l
=1
Δ
V
(
l
)
j
(11)
с ограничениями в виде векторных равенства (8), неравенства (9), (10).
Следует отметить, что в предлагаемой формулировке задача может
иметь весьма высокую размерность. Однако с помощью известного
алгоритма внутренних точек [13] задача линейного программирования
эффективно решается.
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение” 2015. № 2 75

















