Уравнения движения плоского стержня в проекциях на декартовы
оси имеют следующий вид:
⎧⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎩
dQ
x
1
ds
+
q
x
1
= 0;
dQ
x
2
ds
+
q
x
2
= 0;
dM
x
3
ds
+
Q
x
2
cos
ϑ
3
−
Q
x
1
sin
ϑ
3
+
μ
x
3
= 0
.
(2)
На стержень действуют следующие силы инерции:
q
x
1
=
−
ρF
∂
2
u
∂t
2
;
q
x
2
=
−
ρF
∂
2
v
∂ t
2
;
μ
3
=
−
ρJ
33
dω
3
dt
,
где
u
и
v
— продольное ипоперечное перемещения;
ϑ
3
— угол пово-
рота сечения;
ω
3
— угловая скорость поворота сечения;
ρ
— плотность
материала инструмента;
F
— площадь сечения;
J
33
— момент инерции
сечения стержня.
Запишем соотношения упругости
χ
3
−
χ
0
=
M
3
EJ
33
, где
χ
0
— началь-
ная кривизна стержня (
χ
0
= 0
— так как инструмент считаем прямым
стержнем),
χ
3
— приращение кривизны стержня. Это соотношение
справедливо только в связанных осях. Но так как рассматривается
плоская задача, то угол
ϑ
3
, приращение кривизны
χ
3
и изгибающий
момент
M
3
в связанных идекартовых осях совпадают.
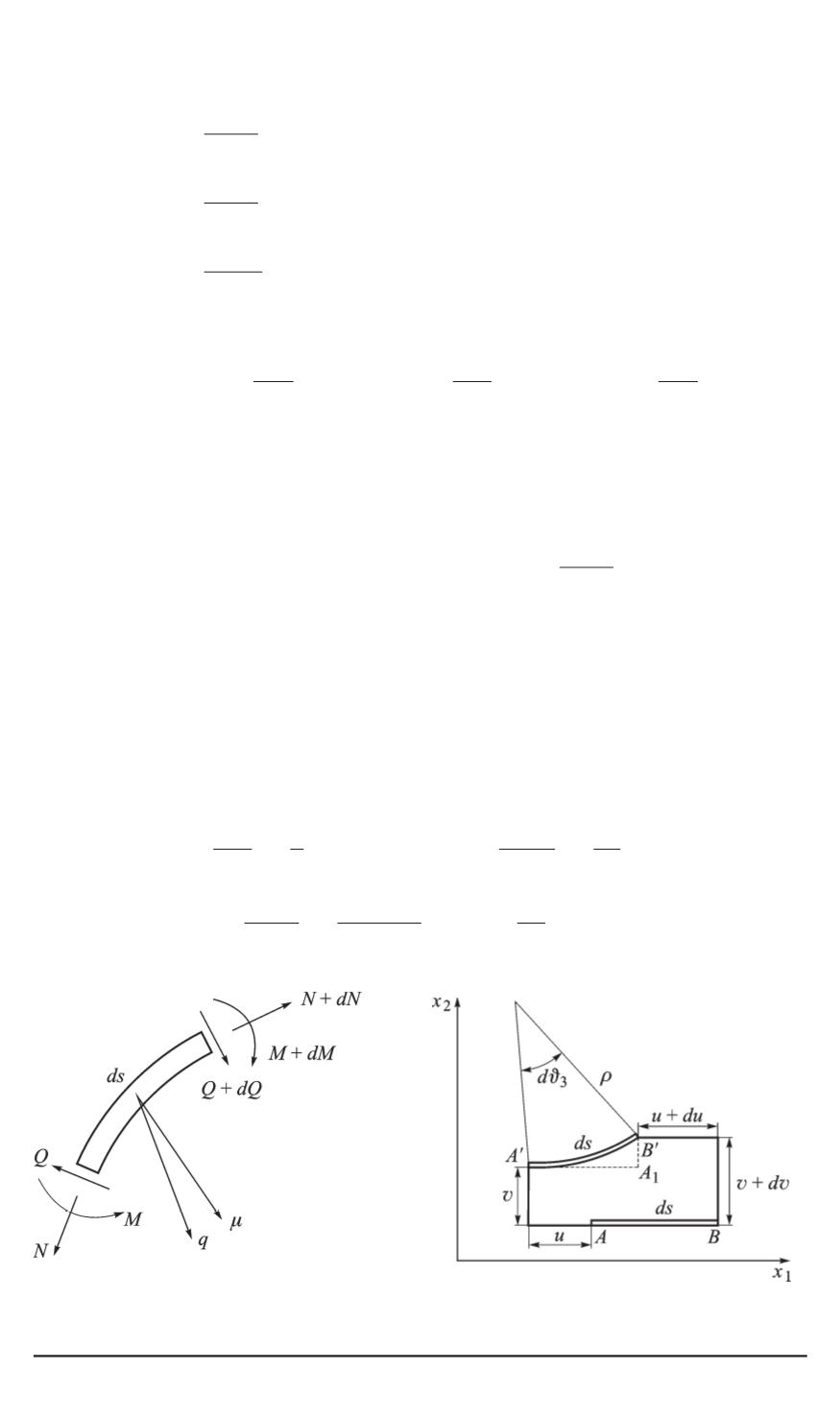
Из геометрии деформирования стержня (рис. 3) и условия нерастя-
жимости получаем следующие кинематические соотношения:
dϑ
3
ds
=
1
ρ
=
χ
3
; sin
ϑ
3
=
B A
1
A B
=
dv
ds
;
cos
ϑ
3
=
A A
1
A B
=
ds
+
du
ds
⇒
du
ds
= cos
ϑ
3
−
1
.
Рис. 2. Внутренние силы и мо-
менты, действующие на элемент
стержня в поперечном сечении
Рис. 3. Элемент стержня в деформи-
рованном состоянии
46 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2009. № 1


