Об устойчивости поведения системы можно судить по максималь-
ному собственному значению матрицы монодромии
ρ
m
= max
j
=1
,n
(
|
μ
j
|
)
.
В случае, если
|
ρ
m
|
<
1
, то прямое положение стебля асимптотически
устойчиво.
Разработан пакет программ, с помощью которого в зависимости от
различных параметров можно построить диаграмму устойчивости.
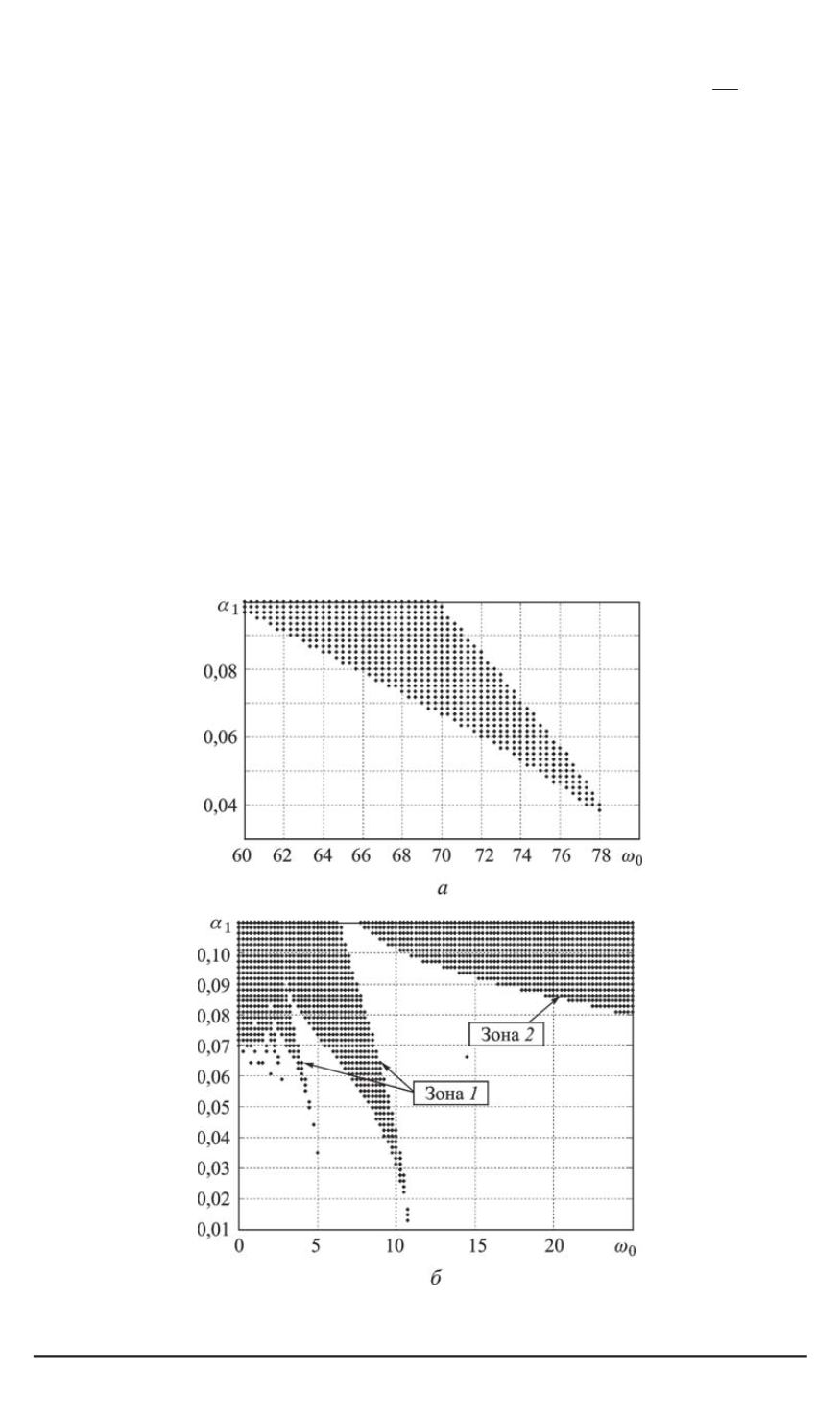
На рис. 7 построены диаграммы устойчивости в зависимости от
амплитуды
α
1
ичастоты возбуждения
ω
0
промежуточной опоры. На
диаграммах точками показаны значения параметров
α
1
и
ω
0
, в кото-
рых решение является неустойчивым. Из графика (см. рис. 7,
а
) видно,
что в определенном диапазоне параметров около удвоенной первой
собственной частоты
(
ρ
1
= 41
,
5
) стебель инструмента теряет устой-
чивость динамическим образом. Таким образом, можно говорить, что
в системе возбуждается параметрический резонанс.
На рис. 7,
б
изображена диаграмма устойчивости при большом зна-
чении осевой силы. Отметим, что при действии силы, близкой к кри-
тической (18), в системе развиваются резонансные колебания, имею-
Рис. 7. Диаграмма устойчивости при
d/l
= 0
,
01
;
α
0
= 0
,
4
(
а
) и
0
,
5
(
б
);
F
р
= 30
(
а
) и 80 (
б
);
b
= 0
,
6
(
а
) и 0 (
б
)
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2009. № 1 55


