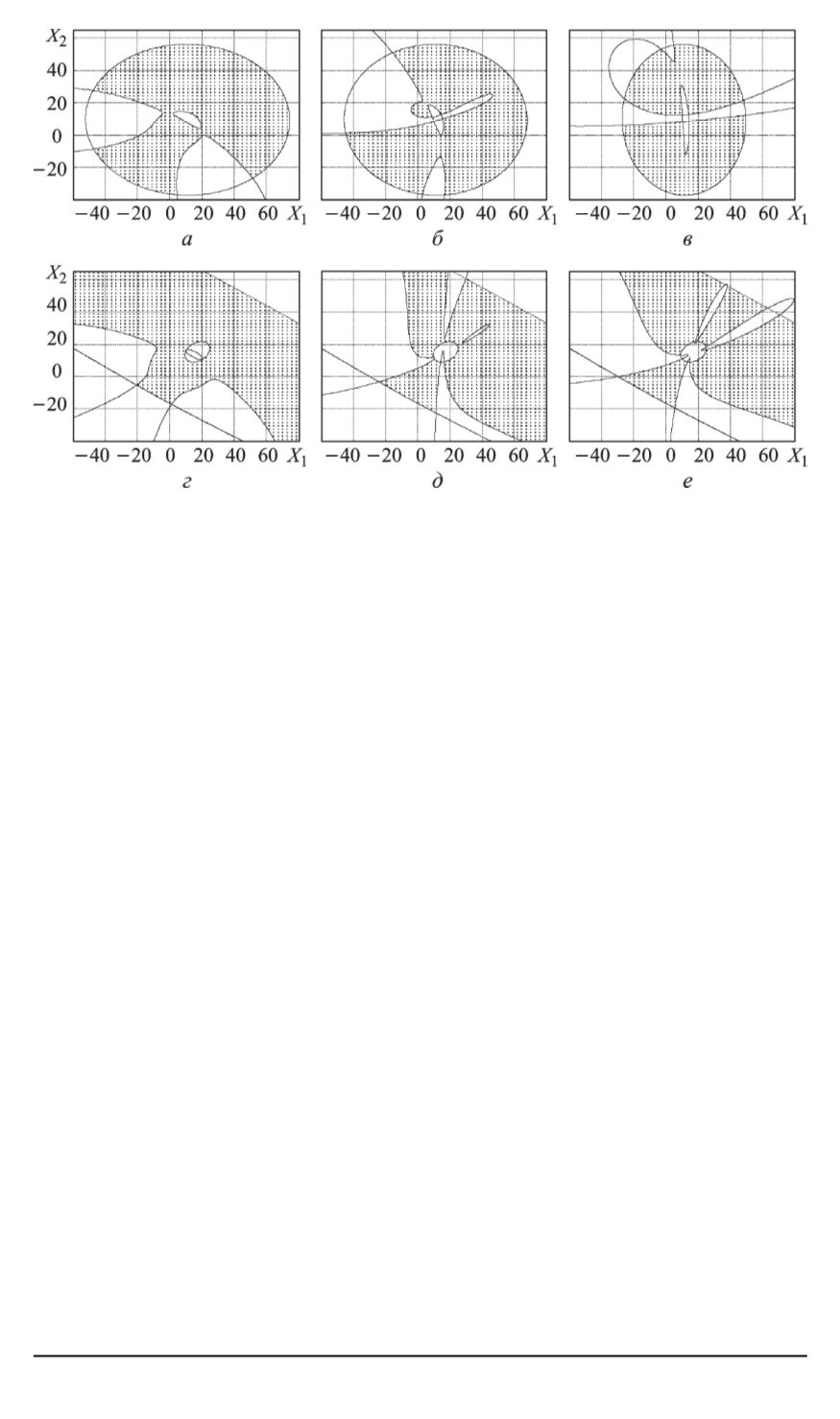
Рис. 4. Влияние взаимного отношения частот осцилляторов на положение
границ устойчивости системы:
ω
1
/ω
2
= 1
(
а,г
); 1,1 (
б,д
); 1,5 (
в,е
);
κ
= 1
(
а–в
); 5 (
г,е
)
аналогичные деформациям при малых отношениях неподвижных и
колеблющихся масс.
Однако в области
ω
1
/ω
2
≈
1
,
08
происходит резкое вытягивание
обеих внешних областей неустойчивости в сторону внутренней, при-
чем после прохождения через внутреннюю (соответствующую частоте
ω
0
)
область неустойчивости каждая из этих областей распадается на
две.
При дальнейшем увеличении отношения частот качественных из-
мененийобластейнеустойчивости не происходит. Область неустойчи-
вости вдоль оси, соответствующейосциллятору с большейчастотой,
растет с ростом этого отношения, а область вдоль другойоси умень-
шается.
Также из анализа этих рисунков можно сделать вывод, что по-
ложение внешних границ области устойчивости при
κ
= 5
, а также
положение границы внутреннейобласти неустойчивости, соответству-
ющейчастоте
ω
0
, от отношения частот практически не зависят.
Анализ влияния параметров объекта управления и автомата
стабилизации.
Проведем анализ влияния на границы устойчивости
аэродинамических характеристик объекта управления и параметров
автомата стабилизации.
Предположим, что характеристики осцилляторов такие же, как и
в предыдущем случае. Влияние аэродинамических характеристик на
границы устойчивости оценим, варьируя значение скоростного напора
набегающего потока
q
. На рис. 5 показаны области устойчивости для
12 ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2010. № 4


