
П.Н. Сильченко, И.В. Кудрявцев, М.М. Михнёв, О.Б. Гоцелюк
12
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 5
Анализ зависимостей (10) показывает, что они определяют только постоян-
ную составляющую напряжений в пластинках 1 и 3 по толщине, равную напря-
жениям, определенным в их срединных плоскостях. Но пластинки 1 и 3 из-за
искривления соединенных с ними пластинок 2 и 4 дополнительно будут испы-
тывать и изгибную деформацию [10, 15]. Следовательно, полученные зависимо-
сти (10) для пластинок 1 и 3 необходимо дополнить выражениями, учитываю-
щими изгибные напряжения от их внецентренного растяжения-сжатия в соста-
ве прямого участка волновода. Искомыми выражениями являются функции
прогибов
,
i
i
i
i
пластинок 1 и 3, которые определяются деформация-
ми их боковых сторон, сопряженных с пластинками 2 и 4 (см. рис. 3,
а
).
Функции прогибов
,
.
i
i
i
i
Рассмотрим деформации
i
-й пластинки
прямого участка (см. рис. 1). Пластинки 2 и 4, согласно (3), изгибаются каждая в
своей плоскости (рис. 4), следовательно, прогибы в их локальных системах ко-
ординат
i i i
Z
(см. рис. 1) из плоскости равны нулю:
2 2 2
4 4 4
,
,
0.
(11)
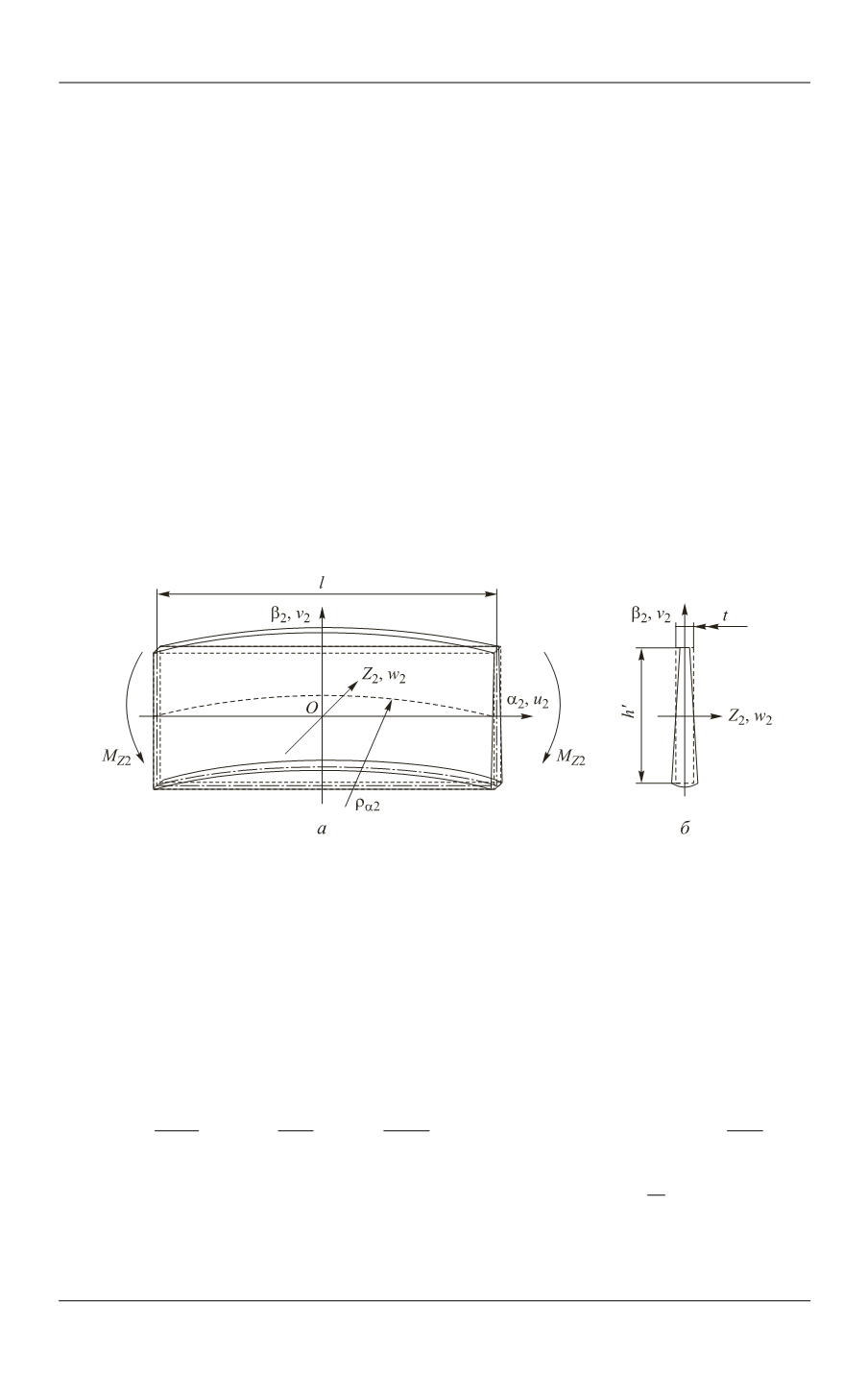
Рис. 4.
Деформация боковой пластинки 2 (
а
) и деформация ее поперечного сечения
в своей плоскости (
б
)
Функции прогибов пластинок 1 и 3 определяются деформациями боковых
сторон сопряженных с ними пластинок 2 и 4 [15]. Поскольку расчетные схемы
для боковых пластинок 2 и 4 эквивалентны, то достаточно рассматривать НДС
только пластинки 2 и только в своей плоскости
2 2
(см. рис. 4).
Согласно зависимостям теории упругости [14], перемещения пластинки 2
можно записать как
2 2
2
2 2
2
,
Z
Z
M
u
EJ
2
2
2
2
2
2 2
,
2
Z
Z
M v
Z
EJ
2
2 2
.
Z
Z
M w Z
EJ
(12)
Перемещения боковой стороны пластинки 2 при
2
2
h
и
2
0
Z
(см.
рис. 4) [15] будут являться и прогибами пластинки 1 по линии их соединения
(см. рис. 1), т. е.
















