
Уточненное решение системы дифференциальных уравнений в задаче изгиба…
ISSN 0236-3941. Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2017. № 5
15
(
H, B
/
L <
0,1) (см. рис. 1). Для пластинок 1 и 3, которые изгибаются (см. рис. 4),
указанная гипотеза неприемлема вследствие сопоставимости их размеров в
продольных
i
и поперечных направлениях
i
(
i
= 1, 3).
Выявленное различие на величину
2
1
является дополнением, которое
уточняет решение, полученное по формуле Навье при изгибе пластинок 1, 3 от
их внецентренного растяжения-сжатия в составе тонкостенного прямоугольно-
го поперечного сечения (см. рис. 4) стержня (прямого участка волновода).
Расчет нормальных напряжений по уточненным зависимостям приводит к
тому, что в местах соединения пластинок напряженное состояние будет неод-
нородным. На рис. 5 приведено распределение нормальных напряжений
1
,
и
2
,
для прямого участка и для области соединения его пласти-
нок 1 и 2 между собой.
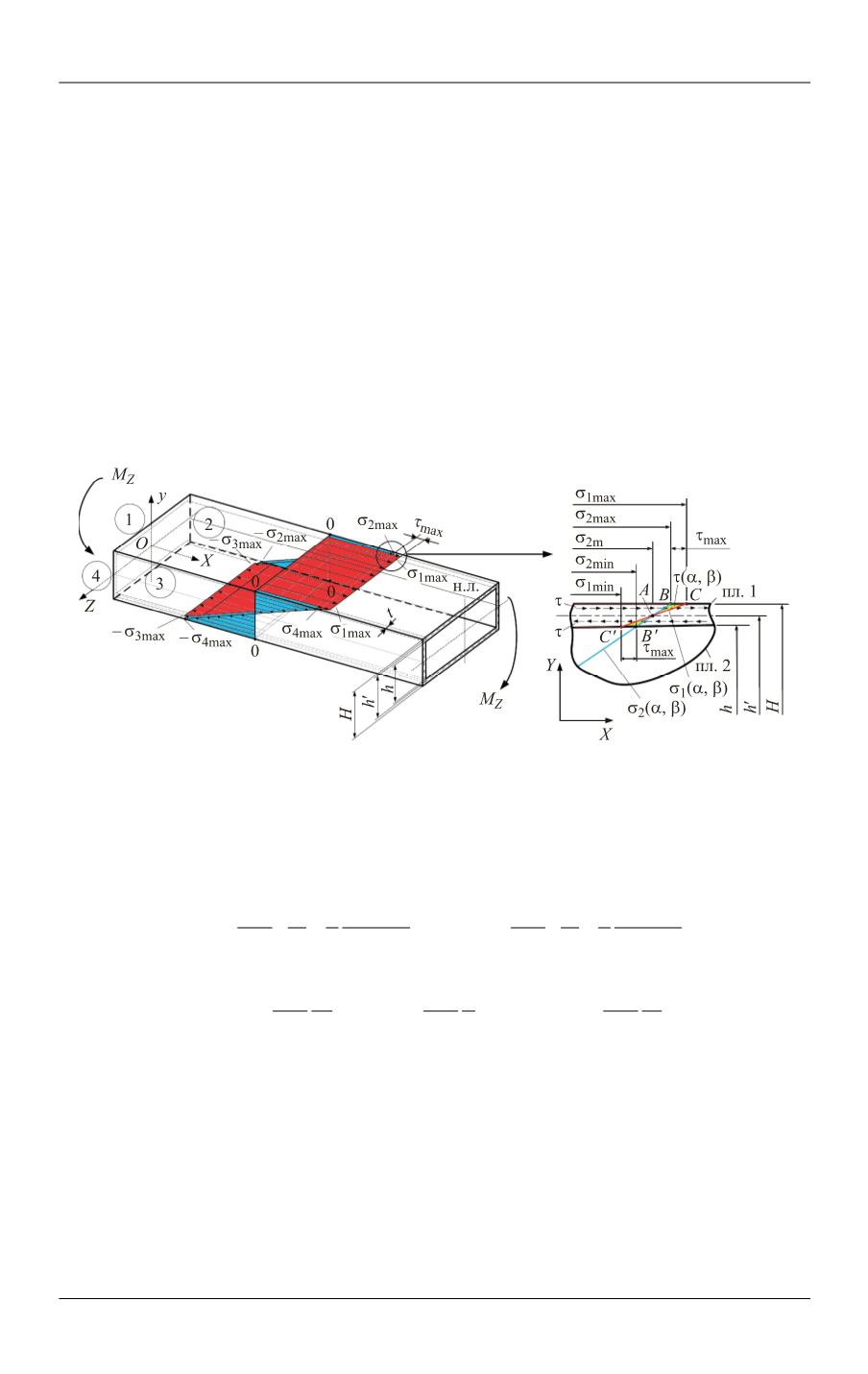
Рис. 5.
Уточненная схема НДС прямого участка при изгибе:
а
— напряжения прямого волновода;
б
— напряжения в месте соединения пластинок 1-2
В месте соединения пластинок 1-2 (рис. 5,
б
) нормальные напряжения в ха-
рактерных точках можно записать как
1max
2
1 ;
2 2 1
Z
Z
M h t
J
1min
2
1 ;
2 2 1
Z
Z
M h t
J
(24)
2 max
;
2
Z
Z
M H
J
2 min
;
2
Z
Z
M h
J
1
2
' .
2
Z
m m
Z
M h
J
(25)
В местах соединения пластинок 2-3, 3-4, 4-1 зависимости (24), (25) для
определения нормальных напряжений будут аналогичными, но с учетом
направлений их локальных систем координат
i i i
Z
(см. рис. 1).
Максимальные касательные напряжения.
Как следует из зависимостей (19)
и (21), для пластинок 1 и 2 нормальные напряжения в месте соединения этих
пластинок скачкообразно изменяются (см. рис. 5). Это вызывает появление в
данном месте касательных напряжений
















